Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Figure 5.8 shows a similar spectrum analysis of two sinusoids
 |
(6.18) |
using the same frequency separation and window lengths. However, now
the sinusoids are 90 degrees out of phase (one sine and one cosine).
Curiously, the top-left case (
 ) now appears to be resolved! However, closer inspection (see
Fig.5.9) reveals that the ``resolved'' spectral peaks
are significantly far away from the sinusoidal frequencies. Another
curious observation is that the lower-left case (
) now appears to be resolved! However, closer inspection (see
Fig.5.9) reveals that the ``resolved'' spectral peaks
are significantly far away from the sinusoidal frequencies. Another
curious observation is that the lower-left case (
 ) appears worse off than it did in
Fig.5.7, and worse than the shorter-window analysis at
the top right of
Fig.5.8. Only the well resolved case at the lower right
(spanning two full cycles of the difference frequency) appears
unaffected by the relative phase of the two sinusoids under analysis.
) appears worse off than it did in
Fig.5.7, and worse than the shorter-window analysis at
the top right of
Fig.5.8. Only the well resolved case at the lower right
(spanning two full cycles of the difference frequency) appears
unaffected by the relative phase of the two sinusoids under analysis.
Figure 5.9 shows the same plots as in
Fig.5.8, but overlaid. From this we can see that the peak
locations are biased in under-resolved cases, both in amplitude
and frequency.
Figure 5.9:
Overlay of the plots in Fig.5.8.
![\includegraphics[width=\textwidth ]{eps/resolvedSinesC2C}](img952.png) |
The preceding figures suggest that, for a rectangular window of length
 , two sinusoids are well resolved when they are separated in
frequency by
, two sinusoids are well resolved when they are separated in
frequency by
 |
(6.19) |
where the frequency-separation
 is in radians per sample. In
cycles per sample, the inequality becomes
is in radians per sample. In
cycles per sample, the inequality becomes
 |
(6.20) |
where the
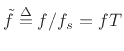 denotes normalized frequency in
cycles per sample. In Hz, we have
denotes normalized frequency in
cycles per sample. In Hz, we have
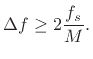 |
(6.21) |
or
 |
(6.22) |
Note that 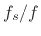 is the number of samples in one period of a
sinusoid at frequency
is the number of samples in one period of a
sinusoid at frequency  Hz, sampled at
Hz, sampled at 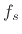 Hz. Therefore, we have
derived a rule of thumb for frequency resolution that requires at
least two full cycles of the difference-frequency under the
rectangular window.
Hz. Therefore, we have
derived a rule of thumb for frequency resolution that requires at
least two full cycles of the difference-frequency under the
rectangular window.
A more detailed study [1] reveals that 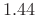 cycles
of the difference-frequency is sufficient to enable fully accurate
peak-frequency measurement under the rectangular window by means of
finding FFT peaks. In §5.5.2 below, additional minimum duration
specifications for resolving closely spaced sinusoids are given for
other window types as well.
cycles
of the difference-frequency is sufficient to enable fully accurate
peak-frequency measurement under the rectangular window by means of
finding FFT peaks. In §5.5.2 below, additional minimum duration
specifications for resolving closely spaced sinusoids are given for
other window types as well.
In principle, we can resolve arbitrarily small frequency
separations, provided
- there is no noise, and
- we are sure we are looking at the sum of two ideal sinusoids under the window.
One method for doing this is described in §5.7.2.
However, in practice, there is almost always some noise and/or
interference from other signals, so we normally prefer to require
sinusoidal frequency separation by on the order of one main-lobe
width or more.
The rectangular window provides an abrupt transition at its edge.
While it remains the optimal window for sinusoidal peak estimation, it
is by no means optimal in all spectrum analysis and/or signal
processing applications involving spectral processing. As discussed in
Chapter 3, windows with a
more gradual transition to zero have lower side-lobe levels, and this
is beneficial for spectral displays and various signal processing
applications based on FFT methods. We will encounter such applications in
later chapters.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() , two sinusoids are well resolved when they are separated in
frequency by
, two sinusoids are well resolved when they are separated in
frequency by
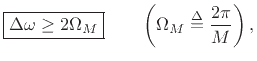
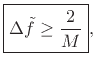
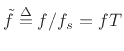 denotes normalized frequency in
cycles per sample. In Hz, we have
denotes normalized frequency in
cycles per sample. In Hz, we have
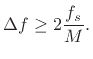

![]() cycles
of the difference-frequency is sufficient to enable fully accurate
peak-frequency measurement under the rectangular window by means of
finding FFT peaks. In §5.5.2 below, additional minimum duration
specifications for resolving closely spaced sinusoids are given for
other window types as well.
cycles
of the difference-frequency is sufficient to enable fully accurate
peak-frequency measurement under the rectangular window by means of
finding FFT peaks. In §5.5.2 below, additional minimum duration
specifications for resolving closely spaced sinusoids are given for
other window types as well.