The likelihood function
![]() is defined as the
probability density function of
is defined as the
probability density function of ![]() given
given
![]() , evaluated at a particular
, evaluated at a particular ![]() , with
, with
![]() regarded as a variable.
regarded as a variable.
In other words, the likelihood function
![]() is just the PDF
of
is just the PDF
of ![]() with a particular value of
with a particular value of ![]() plugged in, and any parameters
in the PDF (mean and variance in this case) are treated as variables.
plugged in, and any parameters
in the PDF (mean and variance in this case) are treated as variables.
For the sinusoidal parameter estimation problem, given a set of
observed data samples ![]() , for
, for
![]() , the likelihood
function is
, the likelihood
function is
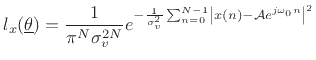 |
(6.50) |
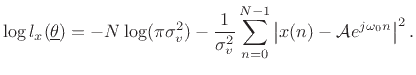 |
(6.51) |
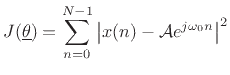 |
(6.52) |