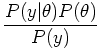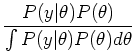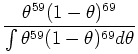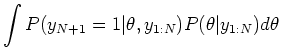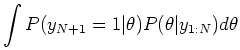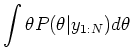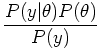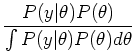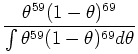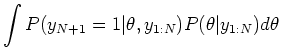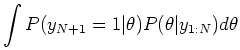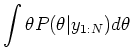Next |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
- Let
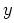 be distributed according to a parametric family:
be distributed according to a parametric family:
 . The goal is, given iid observations
. The goal is, given iid observations
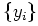 , to estimate
, to estimate 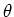 . For instance, let
. For instance, let
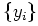 be
a series of coin flips where
be
a series of coin flips where  denotes ``heads'' and
denotes ``heads'' and 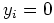 denotes ``tails''. The coin is weighted, so
denotes ``tails''. The coin is weighted, so
 can be
other than
can be
other than 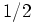 . Let us define
. Let us define
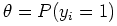 ; our goal is
to estimate
; our goal is
to estimate 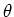 . This simple distribution is given the name
``Bernoulli''.
. This simple distribution is given the name
``Bernoulli''.
- Without prior information, we use the maximum likelihood
approach. Let the observations be
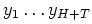 . Let
. Let 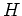 be
the number of heads observed and
be
the number of heads observed and 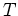 be the number of tails.
be the number of tails.
- Not surprisingly, the probability of heads is estimated as the
empirical frequency of heads in the data sample.
- Suppose we remember that yesterday, using the same coin, we
recorded 10 heads and 20 tails. This is one way to indicate
``prior information'' about
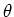 . We simply include these past
trials in our estimate:
. We simply include these past
trials in our estimate:
- As (H+T) goes to infinity, the effect of the past trials will
wash out.
- Suppose, due to computer crash, we had lost the details of the
experiment, and our memory has also failed (due to lack of sleep), that
we forget even the number of heads and tails (which are
the sufficient statistics for the Bernoulli distribution).
However, we believe the probability of heads is about
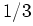 , but this probability itself is somewhat uncertain, since we
only performed 30 trials.
, but this probability itself is somewhat uncertain, since we
only performed 30 trials.
- In short, we claim to have a
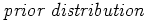 over the probability
over the probability 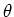 , which represents our prior belief.
Suppose this distribution is
, which represents our prior belief.
Suppose this distribution is 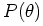 and
and
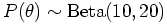 :
:
- Now we observe a new sequence of tosses:
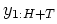 . We may
calculate the posterior distribution
. We may
calculate the posterior distribution
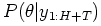 according to Bayes' Rule:
according to Bayes' Rule:
The term
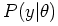 is, as before, the likelihood function of
is, as before, the likelihood function of
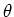 . The marginal
. The marginal  comes by integrating out
comes by integrating out 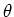 :
:
- To continue our example, suppose we observe in the new
data
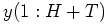 a sequence of 50 heads and 50 tails. The likelihood
becomes:
a sequence of 50 heads and 50 tails. The likelihood
becomes:
- Plugging this likelihood and the prior into the Bayes Rule expression,
and doing he math, obtains the posterior distribution as a
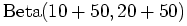 :
:
- Note that the posterior and prior distribution have the same form.
We call such a distribution a conjugate prior. The Beta
distribution is conjugate to the binomial distribution which gives the
likelihood of iid Bernoulli trials. As we will see, a conjugate prior
perfectly captures the results of past experiments. Or, it allows
us to express prior belief in terms of ``invented'' data. More
importantly, conjugacy allows for efficient sequential updating
of the posterior distribution, where the posterior at one stage is
used as prior for the next.
- Key Point The ``output'' of the Bayesian analysis is
not a single estimate of
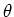 , but rather
the entire posterior distribution. The posterior distribution
summarizes all our ``information'' about
, but rather
the entire posterior distribution. The posterior distribution
summarizes all our ``information'' about 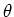 . As we get more data,
if the samples are truly iid, the posterior distribution will become more
sharply peaked about a single value.
. As we get more data,
if the samples are truly iid, the posterior distribution will become more
sharply peaked about a single value.
- Of course, we can use this distribution to make inference
about
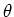 . Suppose an ``oracle'' was to tell
us the true value of
. Suppose an ``oracle'' was to tell
us the true value of 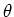 used to generate the samples.
We want to guess
used to generate the samples.
We want to guess 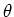 that minimizes the mean squared error between
our guess and the true value. This is the same criterion as in
maximum likelihood estimation. We would choose the mean of the
posterior distribution, because we know conditional mean minimizes
mean square error.
that minimizes the mean squared error between
our guess and the true value. This is the same criterion as in
maximum likelihood estimation. We would choose the mean of the
posterior distribution, because we know conditional mean minimizes
mean square error.
- Let our prior be
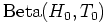 and
and
- The same way, we can do prediction. What is
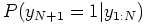 ?
?
Next |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download bayes.pdf
Download bayes_2up.pdf