- False Alarm:
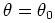 , but
, but

- Miss:
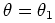 , but
, but
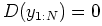
The following facts about Kullback-Leibler distance hold:
-
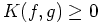 . Equality holds when
. Equality holds when
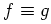 except on
a set of
except on
a set of 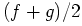 -measure zero. I.E. for a continuous sample
space you can allow difference on sets of Lebesgue measures zero,
for a discrete space you cannot allow any difference.
-measure zero. I.E. for a continuous sample
space you can allow difference on sets of Lebesgue measures zero,
for a discrete space you cannot allow any difference.
-
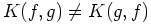 , in general. So the K-L distance is not
a metric. The triangle inequality also fails.
, in general. So the K-L distance is not
a metric. The triangle inequality also fails.
where
We see the threshold is available in closed form, as a function of costs and priors.