The generalized Hamming window family is constructed by multiplying a rectangular window by one period of a cosine. The benefit of the cosine tapering is lower side-lobes. The price for this benefit is that the main-lobe doubles in width. Two well known members of the generalized Hamming family are the Hann and Hamming windows, defined below.
The basic idea of the generalized Hamming family can be seen in the
frequency-domain picture of Fig.3.8. The center dotted
waveform is the aliased sinc function
![]() (scaled rectangular window transform). The
other two dotted waveforms are scaled shifts of the same function,
(scaled rectangular window transform). The
other two dotted waveforms are scaled shifts of the same function,
![]() . The sum of all three dotted waveforms gives
the solid line. We see that
. The sum of all three dotted waveforms gives
the solid line. We see that
![\includegraphics[width=3in]{eps/shiftedSincs}](img353.png) |
In terms of the rectangular window transform
![]() (the zero-phase, unit-amplitude case), this
can be written as
(the zero-phase, unit-amplitude case), this
can be written as
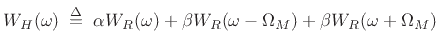 |
(4.15) |
Using the shift theorem (§2.3.4), we can take the inverse transform of the above equation to obtain
| (4.16) |
Choosing various parameters for ![]() and
and ![]() result in
different windows in the generalized Hamming family, some of which
have names.
result in
different windows in the generalized Hamming family, some of which
have names.