Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
To obtain insight into the operation of filter banks implemented using
an FFT, this section will derive the details of the DFT Filter
Bank. More general STFT filter banks are obtained by using different
windows and hop sizes, but otherwise are no different from the basic
DFT filter bank.
The Discrete Fourier Transform (DFT) is defined by [264]
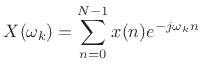 |
(10.4) |
where 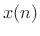 is the input signal at time
is the input signal at time 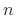 , and
, and
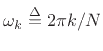 . In this section, we will show how the DFT can be computed
exactly from a bank of
. In this section, we will show how the DFT can be computed
exactly from a bank of  FIR bandpass filters, where each bandpass
filter is implemented as a demodulator followed by a lowpass filter.
We will then find that the inverse DFT is computed by remodulating and
summing the output of this filter bank. In this way, the DFT filter
bank is shown to be a perfect-reconstruction filter bank. The STFT is
then an extension of the DFT filter bank to include non-rectangular
analysis windows
FIR bandpass filters, where each bandpass
filter is implemented as a demodulator followed by a lowpass filter.
We will then find that the inverse DFT is computed by remodulating and
summing the output of this filter bank. In this way, the DFT filter
bank is shown to be a perfect-reconstruction filter bank. The STFT is
then an extension of the DFT filter bank to include non-rectangular
analysis windows 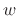 and a downsampling factor
and a downsampling factor 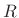 .
.
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
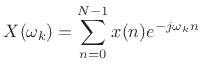
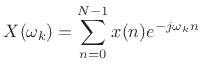
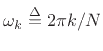 . In this section, we will show how the DFT can be computed
exactly from a bank of
. In this section, we will show how the DFT can be computed
exactly from a bank of