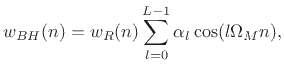 |
(4.26) |
The Blackman-Harris (BH) window family is a straightforward generalization of the Hamming family introduced in §3.2. Recall from that discussion that the generalized Hamming family was constructed using a summation of three shifted and scaled aliased-sinc-functions (shown in Fig.3.8). The Blackman-Harris family is obtained by adding still more shifted sinc functions:
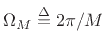 , and
, and  |
(4.27) |
Note that for ![]() , we obtain the rectangular window, and for
, we obtain the rectangular window, and for ![]() ,
the BH family specializes to the generalized Hamming family.
,
the BH family specializes to the generalized Hamming family.