 |
The summation in Eq.(1) cannot be implemented in practice because the ``ideal lowpass filter'' impulse response hs(t) actually extends from minus infinity to infinity. It is necessary in practice to window the ideal impulse response so as to make it finite. This is the basis of the window method for digital filter design [#!DSPC!#,#!RabinerAndGold!#]. While many other filter design techniques exist, the window method is simple and robust, especially for very long impulse responses. In the case of the algorithm presented below, the filter impulse response is very long because it is heavily oversampled. Another approach is to design optimal decimated ``sub-phases'' of the filter impulse response, which are then interpolated to provide the ``continuous'' impulse response needed for the algorithm [#!PutnamAndSmithMohonk97!#].
Figure 3 shows the frequency response of the ideal lowpass filter. This is just the Fourier transform of hs(t).
If we truncate hs(t) at the fifth zero-crossing to the left and the right of the origin, we obtain the frequency response shown in Fig.4. Note that the stopband exhibits only slightly more than 20 dB rejection.
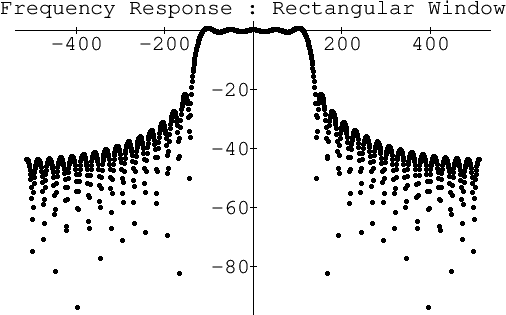 |
If we instead use the Kaiser window [#!Kaiser74!#,#!SmithWinFlt!#] to taper hs(t) to zero by the fifth zero-crossing to the left and the right of the origin, we obtain the frequency response shown in Fig.5. Note that now the stopband starts out close to -80 dB. The Kaiser window has a single parameter which can be used to modify the stop-band attenuation, trading it against the transition width from pass-band to stop-band.
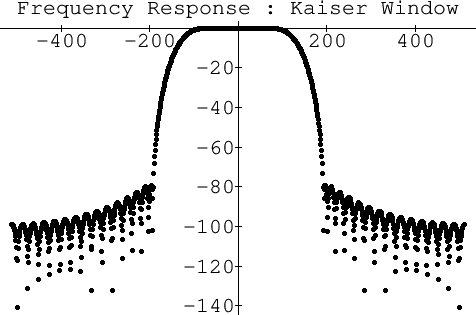 |