Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Flanger Speed and Excursion
As mentioned above, the delay-line length 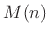 in a digital flanger
is typically modulated by a low-frequency oscillator (LFO).
The oscillator waveform is usually triangular, sinusoidal, or
exponential (triangular on a log-frequency scale). In the sinusoidal
case, we have the following delay variation:
in a digital flanger
is typically modulated by a low-frequency oscillator (LFO).
The oscillator waveform is usually triangular, sinusoidal, or
exponential (triangular on a log-frequency scale). In the sinusoidal
case, we have the following delay variation:
where 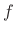 is the ``speed'' (or ``rate'') of the flanger
in cycles per second,
is the ``speed'' (or ``rate'') of the flanger
in cycles per second, 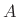 is the ``excursion'' or ``sweep'' (maximum delay swing)
which is often not brought out as a user-controllable parameter, and
is the ``excursion'' or ``sweep'' (maximum delay swing)
which is often not brought out as a user-controllable parameter, and
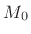 is the average delay length controlling the average notch
density (also not normally brought out as a user-controllable
parameter).
is the average delay length controlling the average notch
density (also not normally brought out as a user-controllable
parameter).
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() in a digital flanger
is typically modulated by a low-frequency oscillator (LFO).
The oscillator waveform is usually triangular, sinusoidal, or
exponential (triangular on a log-frequency scale). In the sinusoidal
case, we have the following delay variation:
in a digital flanger
is typically modulated by a low-frequency oscillator (LFO).
The oscillator waveform is usually triangular, sinusoidal, or
exponential (triangular on a log-frequency scale). In the sinusoidal
case, we have the following delay variation: