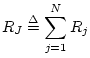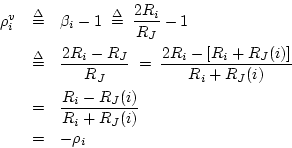Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Physically, the force-wave reflection coefficient seen at port
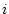 of a series adaptor is due to an impedance step from
of a series adaptor is due to an impedance step from 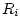 , that
of the port interface, to a new impedance consisting of the series
combination of all other port impedances meeting at the
junction. Let
, that
of the port interface, to a new impedance consisting of the series
combination of all other port impedances meeting at the
junction. Let
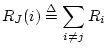 |
(N.35) |
denote this series combination. Then we must have, as
in Eq. (N.25),
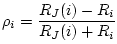 |
(N.36) |
Let's check this ``physical'' derivation against the formal definition
Eq. (N.31) leading to
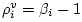 in Eq. (N.33).
Define the total junction impedance as
in Eq. (N.33).
Define the total junction impedance as
This is the series combination of all impedances connected to
the junction. Then by Eq. (N.35),
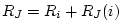 for all
for all
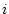 . From Eq. (N.26), the velocity reflection coefficient is given by
. From Eq. (N.26), the velocity reflection coefficient is given by
Since
the result follows.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite and copy this work]
![]() of a series adaptor is due to an impedance step from
of a series adaptor is due to an impedance step from ![]() , that
of the port interface, to a new impedance consisting of the series
combination of all other port impedances meeting at the
junction. Let
, that
of the port interface, to a new impedance consisting of the series
combination of all other port impedances meeting at the
junction. Let
![]() in Eq. (N.33).
Define the total junction impedance as
in Eq. (N.33).
Define the total junction impedance as