Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Acoustic Energy Density
The two forms of energy in a wave are kinetic and
potential:
These are called the acoustic kinetic energy density and the
acoustic potential energy density, respectively.
In a plane wave, where 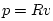 and
and 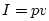 , we have
, we have
Thus, half of the acoustic intensity 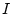 in a plane wave is kinetic,
and the other half is potential:E.11
in a plane wave is kinetic,
and the other half is potential:E.11
Note that acoustic intensity 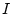 has units of energy per unit
area per unit time while the acoustic energy density
has units of energy per unit
area per unit time while the acoustic energy density 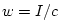 has
units of energy per unit volume.
has
units of energy per unit volume.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite and copy this work]
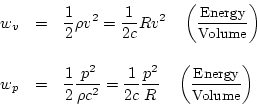
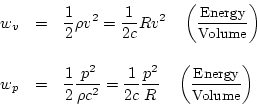
![]() and
and ![]() , we have
, we have
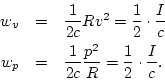
![]() in a plane wave is kinetic,
and the other half is potential:E.11
in a plane wave is kinetic,
and the other half is potential:E.11