![\includegraphics[width=\twidth ]{eps/fbcfar}](img505.png) |
Figure 2.26 shows a family of feedback-comb-filter amplitude responses, obtained using a selection of feedback coefficients.
![\includegraphics[width=\twidth ]{eps/fbcfar}](img505.png) |
Figure 2.27 shows a similar family obtained using negated feedback coefficients; the opposite sign of the feedback exchanges the peaks and valleys in the amplitude response.
![\includegraphics[width=\twidth ]{eps/fbcfiar}](img506.png) |
As introduced in §2.6.2 above, a class of feedback comb filters can be defined as any difference equation of the form
Taking the z transform of both sides and solving for
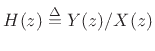 ,
the transfer function of the feedback comb filter is found to be
,
the transfer function of the feedback comb filter is found to be
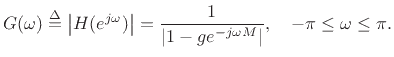
This is plotted in Fig.2.26 for
For ![]() , the feedback-comb amplitude response
reduces to
, the feedback-comb amplitude response
reduces to
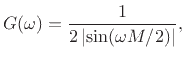
and for
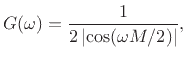
which exactly inverts the amplitude response of the feedforward comb filter with gain
Note that ![]() produces resonant peaks at
produces resonant peaks at
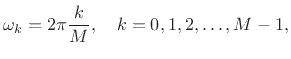
while for