Digital Sinusoid Generators

In [169], three techniques were examined for generating sinusoids digitally by means of recursive algorithms.^C.16 The recursions can be interpreted as implementations of second-order digital resonators in which the damping is set to zero. The three methods considered were (1) the 2D rotation (2DR), or complex multiply (also called the ``coupled form''), (2) the modified coupled form (MCF), or ``magic circle'' algorithm,^C.17which is similar to (1) but with better numerical behavior, and (3) the direct-form, second-order, digital resonator (DFR) with its poles set to the unit circle.

These three recursions may be defined as follows:

$$\begin{array}{crcll} (1) & x_1(n) &=& c_nx_1(n-1) + s_nx_2(n-1) & \\ & x_2(n) &=& -s_nx_1(n-1) + c_nx_2(n-1) & \mbox{(2DR)} \\ [1mm] (2) & x_1(n) &=& x_1(n-1) + \epsilon x_2(n-1) & \\ & x_2(n) &=& -\epsilon x_1(n) + x_2(n-1) & \mbox{(MCF)} \\ [1mm] (3) & x_1(n) &=& 2c_nx_1(n-1) - x_2(n-1) & \\ & x_2(n) &=& x_1(n-1) & \mbox{(DFR)} \end{array}$$

where $c_n\isdef \cos(2\pi f_n T)$ , $s_n\isdef \sin(2\pi f_n T)$ , $f_n$ is the instantaneous frequency of oscillation (Hz) at time sample $n$ , and $T$ is the sampling period in seconds. The magic circle parameter is $\epsilon=2\sin(\pi f_n T)$ .

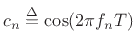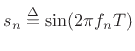The digital waveguide oscillator appears to have the best overall properties yet seen for VLSI implementation. This structure, introduced in [462], may be derived from the theory of digital waveguides (see Appendix C, particularly §C.9, and [437,466]). Any second-order digital filter structure can be used as a starting point for developing a corresponding sinusoidal signal generator, so in this case we begin with the second-order waveguide filter.