Damping and Tuning Parameters

The tuning and damping of the resonator impulse response are governed by the relation

$${\lambda_i}= e^{\frac{T}{\tau}} e^{\pm j\omega T}$$

where $T$ denotes the sampling interval, $\tau$ is the time constant of decay, and $\omega$ is the frequency of oscillation in radians per second. The eigenvalues are presumed to be complex, which requires, from Eq.(C.165),

$$g(1-c^2) \geq\frac{c^2(1-g)^2}{4} \,\,\Rightarrow\,\,c^2 \leq \frac{4g}{(1+g)^2}$$

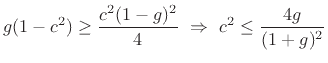
To obtain a specific decay time-constant $\tau$ , we must have

$$\begin{eqnarray*} e^{-2T/\tau} &=& \left\vert{\lambda_i}\right\vert^2 = c^2\left(\frac{1+g}{2}\right)^2 + \left[g(1-c^2) - c^2\left(\frac{1-g}{2}\right)^2\right]\\ &=& g \end{eqnarray*}$$

Therefore, given a desired decay time-constant $\tau$ (and the sampling interval $T$ ), we may compute the damping parameter $g$ for the digital waveguide resonator as

$$\zbox {g = e^{-2T/\tau}.}$$

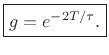
Note that this conclusion follows directly from the determinant analysis of Eq.(C.161), provided it is known that the poles form a complex-conjugate pair.

To obtain a desired frequency of oscillation, we must solve

$$\begin{eqnarray*} \theta = \omega T &=& \tan^{-1}\left[\frac{\sqrt{g(1-c^2) - [c(1-g)/2]^2}}{c(1+g)/2}\right]\\ \,\,\Rightarrow\,\,\tan^2{\theta} &=& \frac{g(1-c^2) - [c(1-g)/2]^2}{[c(1+g)/2]^2} \end{eqnarray*}$$

for $c$ , which yields

$$\zbox { c= \sqrt{\frac{1}{1 + \frac{\tan^2(\theta)(1+g)^2+(1-g)^2}{4g}}} \approx 1 - \frac{\tan^2(\theta)(1+g)^2 + (1-g)^2}{8g}. }$$

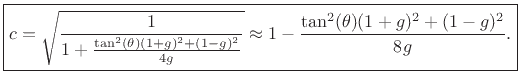
Note that this reduces to $c=\cos(\theta)$ when $g=1$ (undamped case).