Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
When 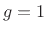 , the eigenvalues reduce to
, the eigenvalues reduce to
Assuming
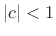 , the eigenvalues can be expressed as
, the eigenvalues can be expressed as
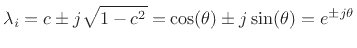 |
(C.164) |
where
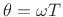 denotes the angular advance per sample of the
oscillator. Since
denotes the angular advance per sample of the
oscillator. Since
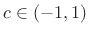 corresponds to the range
corresponds to the range
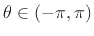 , we see that
, we see that 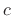 in this range can produce
oscillation at any digital frequency.
in this range can produce
oscillation at any digital frequency.
For
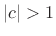 , the eigenvalues are real, corresponding to
exponential growth and/or decay. (The values
, the eigenvalues are real, corresponding to
exponential growth and/or decay. (The values 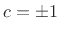 were
excluded above in deriving Eq.(C.165).)
were
excluded above in deriving Eq.(C.165).)
In summary, the coefficient 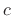 in the digital waveguide oscillator
(
in the digital waveguide oscillator
(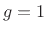 ) and the frequency of sinusoidal oscillation
) and the frequency of sinusoidal oscillation 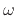 is simply
is simply
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() , the eigenvalues reduce to
, the eigenvalues reduce to
![]() , the eigenvalues are real, corresponding to
exponential growth and/or decay. (The values
, the eigenvalues are real, corresponding to
exponential growth and/or decay. (The values ![]() were
excluded above in deriving Eq.(C.165).)
were
excluded above in deriving Eq.(C.165).)
![]() in the digital waveguide oscillator
(
in the digital waveguide oscillator
(![]() ) and the frequency of sinusoidal oscillation
) and the frequency of sinusoidal oscillation ![]() is simply
is simply