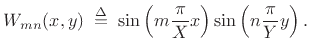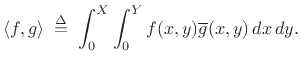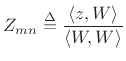Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
We often wish to find solutions of the 2D wave equation that obey
certain known boundary conditions. An example is transverse
waves on an ideal elastic membrane, rigidly clamped on its boundary to
form a rectangle with dimensions  meters.
meters.
Similar to the derivation of Eq.(B.51), we can subtract
the second sinusoidal traveling wave from the first to yield
which satisfies the zero-displacement boundary condition along the 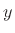 axis. If we restrict the wavenumber
axis. If we restrict the wavenumber 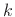 to the set
to the set 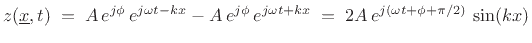 , where
, where
 is any positive integer, then we also satisfy the boundary
condition along the line parallel to the
is any positive integer, then we also satisfy the boundary
condition along the line parallel to the 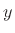 axis at
axis at 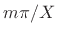 . Similar
standing waves along
. Similar
standing waves along 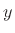 will satisfy both boundary conditions along
will satisfy both boundary conditions along
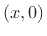 and
and 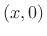 .
.
Note that we can also use products of horizontal and vertical
standing waves
because, when taking the partial derivative with respect to  , the
term
, the
term 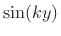 is simply part of the constant coefficient, and vice
versa.
is simply part of the constant coefficient, and vice
versa.
To build solutions to the wave equation that obey all of the boundary
conditions, we can form linear combinations of the above standing-wave
products having zero displacement (``nodes'') along all four boundary
lines:
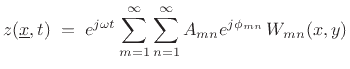 |
(B.52) |
where
By construction, all linear combinations of the form Eq.(B.52)
are solutions of the wave equation that satisfy the zero boundary
conditions along the rectangle 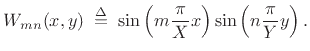 -
-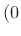 -
-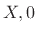 . Since sinusoids at
different frequencies are orthogonal,
the solution building-blocks
. Since sinusoids at
different frequencies are orthogonal,
the solution building-blocks
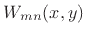 are orthogonal under the
inner product
are orthogonal under the
inner product
It remains to be shown that the set of functions
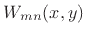 is
complete, that is, that they form a basis for the set of
all solutions to the wave equation satisfying the boundary
conditions. Given that, we can solve the problem of arbitrary
initial conditions. That is, given any initial
is
complete, that is, that they form a basis for the set of
all solutions to the wave equation satisfying the boundary
conditions. Given that, we can solve the problem of arbitrary
initial conditions. That is, given any initial 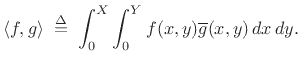 over the
membrane (subject to the boundary conditions, of course), we can find
the amplitude of each excited mode by simple orthogonal projection:
over the
membrane (subject to the boundary conditions, of course), we can find
the amplitude of each excited mode by simple orthogonal projection:
Showing completeness of the basis
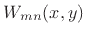 in the desired solution
space is a special case (zero boundary conditions) of the problem of
showing that the 2D Fourier series expansion is complete in the space
of all continuous rectangular surfaces.
in the desired solution
space is a special case (zero boundary conditions) of the problem of
showing that the 2D Fourier series expansion is complete in the space
of all continuous rectangular surfaces.
The Wikipedia page (as of 1/31/10) on the Helmholtz equation
provides a nice ``entry point'' on the above topics and further
information.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() meters.
meters.