Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
TDL for Parallel Processing
When multiplies and additions can be performed in parallel, the
computational complexity of a tapped delay line is
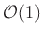 multiplies and
multiplies and
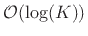 additions, where
additions, where 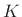 is the number of
taps. This computational complexity is achieved by arranging the
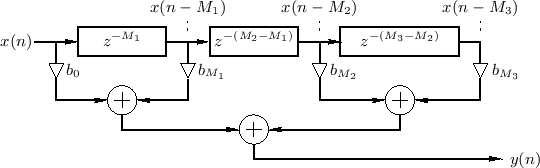
additions into a binary tree, as shown in Fig.2.21 for the
case
is the number of
taps. This computational complexity is achieved by arranging the
additions into a binary tree, as shown in Fig.2.21 for the
case 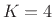 .
.
Figure 2.21:
An example Tapped Delay Line (TDL),
with additions organized into a binary tree for maximized
parallel computation.
 |
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() multiplies and
multiplies and
![]() additions, where
additions, where ![]() is the number of
taps. This computational complexity is achieved by arranging the
additions into a binary tree, as shown in Fig.2.21 for the
case
is the number of
taps. This computational complexity is achieved by arranging the
additions into a binary tree, as shown in Fig.2.21 for the
case ![]() .
.
