General Causal FIR Filters

The most general case of a TDL having a tap after every delay element is the general causal finite-impulse-response (FIR) filter, shown in Fig.1.16. It is restricted to be causal because the output $y(n)$ may not depend on ``future'' input samples $x(n+1)$, $x(n+2)$, etc. The FIR filter may also be called a transversal filter. FIR filters are described in greater detail in [455].

Figure 1.16: The general, causal, finite-impulse-response (FIR) digital filter.

The difference equation for the $M$th-order FIR filter in Fig.1.16 is, by inspection,

$$y(n) = b_0 x(n) + b_1 x(n-1) + b_2 x(n-2) + b_3 x(n-3) + \cdots + b_M x(n-M)$$

and the transfer function is

$$H(z) = b_0 + b_1 z^{-1} + b_2 z^{-2} + b_3 z^{-3} + \cdots + b_M z^{-M} = \sum_{m=0}^M b_m z^{-m} \isdef B(z).$$

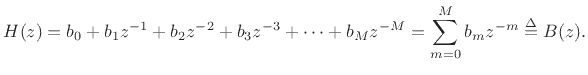
The STK class for implementing arbitrary direct-form FIR filters is called Filter. In Matlab and Octave, the built-in function filter is normally used.