Rotational Kinetic Energy Revisited

If a point-mass is located at $\underline {x}$ and is rotating about an axis-of-rotation $\underline {\tilde {\omega }}$ with angular velocity $\omega$ , then the distance from the rotation axis to the mass is $r= \vert\vert\,\underline{x}-{\cal P}_{\underline{\tilde{\omega}}}(\underline{x})\,\vert\vert = \vert\vert\,(\mathbf{E}-\underline{\tilde{\omega}}\underline{\tilde{\omega}}^T)\underline{x}\,\vert\vert$ , or, in terms of the vector cross product, $r= \vert\vert\,\underline{\tilde{\omega}}\times\underline{x}\,\vert\vert$ . The tangential velocity of the mass is then $r\omega$ , so that the kinetic energy can be expressed as (cf. Eq.(B.23))

$$E_R \eqsp \frac{1}{2}m\left\Vert\,\underline{\tilde{\omega}}\times\underline{x}\,\right\Vert^2\omega^2 \eqsp \frac{1}{2}I\omega^2 \protect$$ (B.25)

where

$$I \eqsp m\left\Vert\,\underline{\tilde{\omega}}\times\underline{x}\,\right\Vert^2.$$

In a collection of $N$ masses $m_i$ having velocities $\underline{v}_i$ , we of course sum the individual kinetic energies to get the total kinetic energy.

Finally, we may also write the rotational kinetic energy as half the inner product of the angular-velocity vector and the angular-momentum vector:^B.27

$$E_R \eqsp \frac{1}{2}\, \underline{\omega}\cdot \underline{L}\eqsp \frac{1}{2} I \omega^2,$$

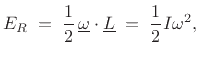
where the second form (introduced above in Eq.(B.7)) derives from the vector-dot-product form by using Eq.(B.20) and Eq.(B.22) to establish that $\underline{\omega}\cdot\underline{L}=\underline{\omega}\cdot \mathbf{I}\underline{\omega}= \underline{\omega}^T\mathbf{I}\underline{\omega}= \omega^2 \underline{\tilde{\omega}}^T\mathbf{I}\underline{\tilde{\omega}}= I \omega^2$ .