![\includegraphics[width=4in]{eps/SchematicWaveguideMesh}](img4079.png) |
Figure C.34 shows the basic layout of the rectilinear 2D waveguide mesh. It can be thought of as simulating a plane using 1D digital waveguides in the same way that a tennis racket acts as a membrane composed of 1D strings.
At each node (string intersection), we have the following simple formula for the
node velocity ![]() in terms of the four incoming traveling-wave components:
in terms of the four incoming traveling-wave components:
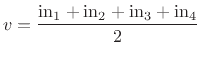
By continuity of velocity in a series connection (all string endpoints must move together at the node), the outgoing velocity-wave components must be given by
This computation is performed by the following Faust [155] program:
import("math.lib");
process=bus(4)<:par(i,4,*(-1)),(bus(4):>*(.5)<:bus(4)):>bus(4);