It turns out only one multiply is needed to implement
three-port adaptors (scattering junctions) having a reflection-free
port. The derivation is very similar to deriving the one-multiply
two-port scattering junction from the four-multiply Kelly-Lochbaum
scattering junction, as discussed in Fig.![]() .
.
Let's begin with the scattering relations in terms of the alpha
parameters introduced in §F.2.2 for a parallel junction
of any number of ports:
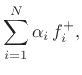 |
(F.23) | ||
| (F.24) |
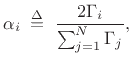
and
Here we wish to focus on the three-port case ![]() . To connect with
our previous example, set
. To connect with
our previous example, set ![]() ,
, ![]() , and
, and ![]() . When
port A is reflection-free, we have the constraint that
. When
port A is reflection-free, we have the constraint that
![]() (
(
![]() ). Scattering
relations are unchanged when all port impedances are divided by the
same positive number, so divide through by
). Scattering
relations are unchanged when all port impedances are divided by the
same positive number, so divide through by ![]() to obtain
to obtain
![]() , and
, and
![]() . With
. With
![]() , we have
, we have
![]() , and
, and
![]() . In other words, there is only
one degree of freedom,
. In other words, there is only
one degree of freedom,
![]() for the three-port
parallel junction with a reflection-free port.
for the three-port
parallel junction with a reflection-free port.
The alpha parameters become
![]() ,
,
![]() ,
and
,
and
![]() , so that the scattering formulas simplify to
, so that the scattering formulas simplify to
| (F.25) | |||
| (F.26) |
| (F.27) | |||
| (F.28) | |||
| (F.29) | |||
| (F.30) | |||
| (F.31) | |||
| (F.32) |