Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Alpha Parameters
It is customary in the wave digital filter literature to define the
alpha parameters as
 |
(F.14) |
where
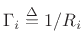 are the admittances of the wave digital
element interfaces (or ``reference admittances,'' in WDF terminology).
In terms of the alpha parameters, the force-wave parallel adaptor
performs the following computations:
are the admittances of the wave digital
element interfaces (or ``reference admittances,'' in WDF terminology).
In terms of the alpha parameters, the force-wave parallel adaptor
performs the following computations:
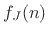 |
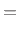 |
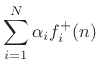 (Common Junction Force) (Common Junction Force)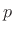 |
(F.15) |
 |
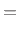 |
 (Outgoing Force Waves) (Outgoing Force Waves)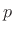 |
(F.16) |
We see that 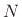 multiplies and
multiplies and  additions are required.
additions are required.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]

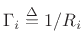 are the admittances of the wave digital
element interfaces (or ``reference admittances,'' in WDF terminology).
In terms of the alpha parameters, the force-wave parallel adaptor
performs the following computations:
are the admittances of the wave digital
element interfaces (or ``reference admittances,'' in WDF terminology).
In terms of the alpha parameters, the force-wave parallel adaptor
performs the following computations: