Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
The matched z transformation uses the same pole-mapping
Eq.(8.2) as in the impulse-invariant method, but the zeros
are handled differently. Instead of only mapping the poles of the
partial fraction expansion and letting the zeros fall where they may,
the matched z transformation maps both the poles and zeros in the
factored form of the transfer function [365, pp.
224-226].
The factored form [452] of a transfer function
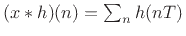 |
(9.3) |
can be written as
 |
(9.4) |
The matched z transformation is carried out by replacing each first-order
term of the form 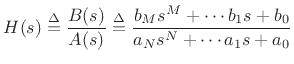 by its digital equivalent
by its digital equivalent
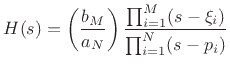 , i.e.,
, i.e.,
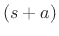 |
(9.5) |
to get
 |
(9.6) |
where the free gain 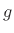 is introduced to implement the desired normalization, such as matching dc gain.
Note that the matched z transformation normally yields different digital zeros
than the impulse-invariant method. The impulse-invariant method is
generally considered superior to the matched z transformation
[346].
is introduced to implement the desired normalization, such as matching dc gain.
Note that the matched z transformation normally yields different digital zeros
than the impulse-invariant method. The impulse-invariant method is
generally considered superior to the matched z transformation
[346].
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]