Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
A finite difference approximation (FDA) approximates derivatives with
finite differences, i.e.,
![$\displaystyle \frac{d}{dt} x(t) \isdefs \lim_{\delta\to 0} \frac{x(t) - x(t-\delta)}{\delta} \;\approx\; \frac{x(n T)-x[(n-1)T]}{T} \protect$](img1646.png) |
(8.2) |
for sufficiently small 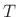 .8.5
.8.5
Equation (7.2) is also known as the backward difference
approximation of differentiation.
See §C.2.1 for a discussion of using the FDA to model ideal
vibrating strings.
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![$\displaystyle \frac{d}{dt} x(t) \isdefs \lim_{\delta\to 0} \frac{x(t) - x(t-\delta)}{\delta} \;\approx\; \frac{x(n T)-x[(n-1)T]}{T} \protect$](img1646.png)