Incorporating Control Motion

Let $y_m(t)$ denote the vertical position of the mass in Fig.9.22. (We still assume $m=\infty$ .) We can think of $y_m$ as the position of the control point on the plectrum, e.g., the position of the ``pinch-point'' holding the plectrum while plucking the string. In a harpsichord, $y_m$ can be considered the jack position [350].

Also denote by $L$ the rest length of the spring $k$ in Fig.9.22, and let $y_e \isdeftext y_m+L$ denote the position of the ``end'' of the spring while not in contact with the string. Then the plectrum makes contact with the string when

$$y_e(t) \ge y(t)$$

where $y(t)$ denotes string vertical position at the plucking point $x_p$ . This may be called the collision detection equation.

Let the subscripts $1$ and $2$ each denote one side of the scattering system, as indicated in Fig.9.23. Then, for example, $y_1=y_1^-+y_1^+$ is the displacement of the string on the left (side $1$ ) of plucking point, and $y_2$ is on the right side of $x_p$ (but still located at point $x_p$ ). By continuity of the string, we have

$$y(t)\eqsp y_1(t)\eqsp y_2(t).$$

When the spring engages the string ($y_e > y$ ) and begins to compress, the upward force on the string at the contact point is given by

$$f_k \eqsp k\cdot (y_e-y)$$

where again $y_e=y_m+L$ . The force $f_k$ is applied given $y_e\ge y$ (spring is in contact with string) and given $f_k < f_{\mbox{\tiny max}}$ (the force at which the pluck releases in a simple max-force model).^10.15 For $y_e< y$ or $f_k \ge f_{\mbox{\tiny max}}$ the applied force is zero and the entire plucking system disappears to leave $y_1^- = y_2^-$ and $y_2^+=y_1^+$ , or equivalently, the force reflectance becomes $\hat{\rho}_f=0$ and the transmittance becomes $\hat{\tau}_f=1$ .

During contact, force equilibrium at the plucking point requires (cf. §9.3.1)

$$0 \eqsp f_1+f_k-f_2 \protect$$ (10.25)

where $f_i \isdeftext -Ky'_i \isdeftext -K\partial y_i/\partial x$ as usual (§6.1), with $K$ denoting the string tension. Using Ohm's laws for traveling-wave components (p. ), we have

$$f_i \eqsp f_i^++f_i^- \eqsp Rv_i^+ - Rv_i^-,$$

where $R=\sqrt{K\epsilon }$ denotes the string wave impedance (p. ). Solving Eq.(9.25) for the velocity at the plucking point yields

$$v \eqsp v_1^+ + v_2^- + \frac{1}{2R} f_k,$$

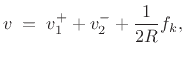
or, for displacement waves,

$$y \eqsp y_1^+ + y_2^- + \frac{1}{2R} \int_t f_k. \protect$$ (10.26)

Substituting $f_k = k\cdot (y_e-y)$ and taking the Laplace transform yields

$$Y(s) \eqsp Y_1^+(s) + Y_2^-(s) + \frac{1}{2R} \frac{F_k(s)}{s} \eqsp Y_1^+(s) + Y_2^-(s) + \frac{k}{2Rs}\left[Y_e(s) - Y(s)\right].$$

Solving for $Y(s)$ and recognizing the force reflectance $\hat{\rho}_f(s)$ gives

$$\begin{eqnarray*} Y(s) &=& \left[1-\hat{\rho}_f(s)\right]\cdot \left[Y_1^+(s)+Y_2^-(s)\right]+\hat{\rho}_f(s)Y_e(s)\\ &=& \left[Y_1^+(s)+Y_2^-(s)\right] + \hat{\rho}_f(s)\cdot \left\{Y_e(s) - \left[Y_1^+(s)+Y_2^-(s)\right]\right\}, \end{eqnarray*}$$

where, as first noted at Eq.(9.24) above,

$$\hat{\rho}_f(s) \isdefs \frac{\left(\frac{k}{s}+R\right) - R}{\left(\frac{k}{s}+R\right) + R} \eqsp \frac{\frac{k}{s}}{2R+\frac{k}{s}} \eqsp \frac{\frac{k}{2R}}{s+\frac{k}{2R}}.$$

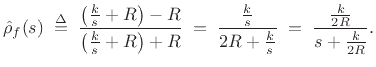
We can thus formulate a one-filter scattering junction as follows:

$$\begin{eqnarray*} Y_d^+ &=& Y_e - \left(Y_1^+ + Y_2^-\right)\\ [5pt] Y_1^- &=& Y_2^- + \hat{\rho}_f Y_d^+\\ [5pt] Y_2^+ &=& Y_1^+ + \hat{\rho}_f Y_d^+. \end{eqnarray*}$$

This system is diagrammed in Fig.9.24. The manipulation of the minus signs relative to Fig.9.23 makes it convenient for restricting $y_d^+(t)$ to positive values only (as shown in the figure), corresponding to the plectrum engaging the string going up. This uses the approximation $y_1(t)=y_2(t)\approx y_1^+(t)+y_2^-(t)$ , which is exact when $\hat{\rho}_f=0$ , i.e., when the plectrum does not affect the string displacement at the current time. It is therefore exact at the time of collision and also applicable just after release. Similarly, $y_d^+(t)>f_{\mbox{\tiny max}}/k$ can be used to trigger a release of the string from the plectrum.

Figure 9.24: Instantaneous spring displacement-wave scattering model driven by the spring edge $y_e(t)=y_m(t)+L$ .