| (B.45) |
The ideal gas law can be written as
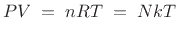
The alternate form ![]() comes from the statistical
mechanics derivation in which
comes from the statistical
mechanics derivation in which ![]() is the number of gas molecules in
the volume, and
is the number of gas molecules in
the volume, and ![]() is Boltzmann's constant. In this
formulation (the kinetic theory of ideal gases), the
average kinetic
energy of the gas molecules is given by
is Boltzmann's constant. In this
formulation (the kinetic theory of ideal gases), the
average kinetic
energy of the gas molecules is given by ![]() . Thus,
temperature is proportional to average kinetic energy of the
gas molecules, where the kinetic energy of a molecule
. Thus,
temperature is proportional to average kinetic energy of the
gas molecules, where the kinetic energy of a molecule ![]() with
translational speed
with
translational speed ![]() is given by
is given by ![]() .
.
In an ideal gas, the molecules are like little rubber balls (or rubbery assemblies of rubber balls) in a weightless vacuum, colliding with each other and the walls elastically and losslessly (an ``ideal rubber''). Electromagnetic forces among the molecules are neglected, other than the electron-orbital repulsion producing the elastic collisions; in other words, the molecules are treated as electrically neutral far away. (Gases of ionized molecules are called plasmas.)
The mass ![]() of the gas in volume
of the gas in volume ![]() is given by
is given by ![]() , where
, where ![]() is
the molar mass of the gass (about 29 g per mole for air). The
air density is thus
is
the molar mass of the gass (about 29 g per mole for air). The
air density is thus ![]() so that we can write
so that we can write
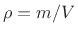
That is, pressure
We normally do not need to consider the (nonlinear) ideal gas law in
audio acoustics because it is usually linearized about some
ambient pressure ![]() . The physical pressure is then
. The physical pressure is then ![]() , where
, where
![]() is the usual acoustic pressure-wave variable. That is, we are
only concerned with small pressure perturbations
is the usual acoustic pressure-wave variable. That is, we are
only concerned with small pressure perturbations ![]() in typical
audio acoustics situations, so that, for example, variations in volume
in typical
audio acoustics situations, so that, for example, variations in volume
![]() and density
and density ![]() can be neglected. Notable exceptions include
brass instruments which can achieve nonlinear sound-pressure regions,
especially near the mouthpiece [199,52].
Additionally, the aeroacoustics of air jets is nonlinear
[197,534,535,536,102,101].
can be neglected. Notable exceptions include
brass instruments which can achieve nonlinear sound-pressure regions,
especially near the mouthpiece [199,52].
Additionally, the aeroacoustics of air jets is nonlinear
[197,534,535,536,102,101].