Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Differentiator Filter Bank
Since, in the time domain, a Taylor series expansion of
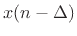 about time
about time  gives
gives
where 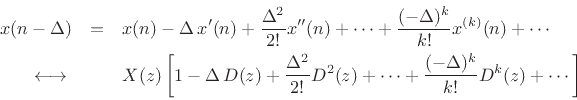 denotes the transfer function of the ideal differentiator,
we see that the
denotes the transfer function of the ideal differentiator,
we see that the  th filter in Eq.(4.10) should approach
th filter in Eq.(4.10) should approach
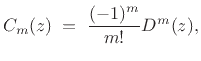 |
(5.12) |
in the limit, as the number of terms 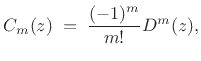 goes to infinity.
In other terms, the coefficient
goes to infinity.
In other terms, the coefficient 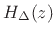 of
of 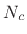 in the polynomial
expansion Eq.(4.10) must become proportional to the
in the polynomial
expansion Eq.(4.10) must become proportional to the
 th-order differentiator as the polynomial order increases.
For any finite
th-order differentiator as the polynomial order increases.
For any finite 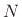 , we expect
, we expect 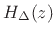 to be close to some scaling of
the
to be close to some scaling of
the  th-order differentiator. Choosing
th-order differentiator. Choosing 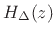 as in Eq.(4.12)
for finite
as in Eq.(4.12)
for finite 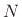 gives a truncated Taylor series approximation of
the ideal delay operator in the time domain [185, p. 1748].
Such an approximation is ``maximally smooth'' in the time domain, in
the sense that the first
gives a truncated Taylor series approximation of
the ideal delay operator in the time domain [185, p. 1748].
Such an approximation is ``maximally smooth'' in the time domain, in
the sense that the first 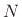 derivatives of the interpolation error
are zero at
derivatives of the interpolation error
are zero at 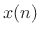 .5.7 The
approximation error in the time domain can be said to be
maximally flat.
.5.7 The
approximation error in the time domain can be said to be
maximally flat.
Farrow structures such as Fig.4.19 may be used to implement any
one-parameter filter variation in terms of several constant
filters. The same basic idea of polynomial expansion has been applied
also to time-varying filters (replace 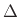 with
with 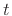 ).
).
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() about time
about time ![]() gives
gives
![\begin{eqnarray*}
x(n-\Delta)
&=& x(n) -\Delta\, x^\prime(n)
+ \frac{\Delta^2}{2!} x^{\prime\prime}(n)
+ \cdots
+ \frac{(-\Delta)^k}{k!}x^{(k)}(n)
+ \cdots \nonumber \\
\;\longleftrightarrow\;&&
X(z)\left[1 - \Delta\, D(z) + \frac{\Delta^2}{2!} D^2(z) + \cdots
+ \frac{(-\Delta)^k}{k!}D^k(z) + \cdots \right]
\end{eqnarray*}](img1103.png)
![]() denotes the transfer function of the ideal differentiator,
we see that the
denotes the transfer function of the ideal differentiator,
we see that the ![]() th filter in Eq.(4.10) should approach
th filter in Eq.(4.10) should approach
![]() with
with ![]() ).
).