Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
As discussed in §E.2, the traveling-wave decomposition
Eq.(E.4) defines a linear transformation Eq.(E.10) from the DW
state to the FDTD state:
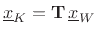 |
(E.27) |
Since
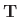 is invertible, it qualifies as a linear transformation
for performing a change of coordinates for the state space.
Substituting Eq.(E.27) into the FDTD
state space model Eq.(E.24) gives
is invertible, it qualifies as a linear transformation
for performing a change of coordinates for the state space.
Substituting Eq.(E.27) into the FDTD
state space model Eq.(E.24) gives
Multiplying through Eq.(E.28) by
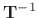 gives a new state-space
representation of the same dynamic system
which we will show is in fact the DW model of Fig.E.2:
gives a new state-space
representation of the same dynamic system
which we will show is in fact the DW model of Fig.E.2:
where
To verify that the DW model derived in this manner is the
computation diagrammed in Fig.E.2, we may write down the
state transition matrix for one subgrid from the figure to obtain
the permutation matrix
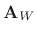 ,
,
![$\displaystyle \underbrace{\left[\! \begin{array}{l} \qquad\vdots \\ y^{+}_{n+2,m-2} \\ y^{-}_{n+2,m-2} \\ y^{+}_{n+2,m} \\ y^{-}_{n+2,m} \\ y^{+}_{n+2,m+2} \\ y^{-}_{n+2,m+2} \\ \qquad\vdots \end{array} \!\right]}_{\underline{x}_W(n+2)} \!\leftarrow\! \underbrace{\left[\! \begin{array}{cccccccccccc} \cdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \cdots & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots\\ \cdots & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & \cdots\\ \cdots & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots\\ \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & \cdots\\ \cdots & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & \cdots\\ \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & \cdots\\ \cdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \end{array} \!\right]}_{\mathbf{A}_W} \! \underbrace{\left[\! \begin{array}{l} \quad\vdots \\ y^{+}_{n,m-4} \\ y^{-}_{n,m-4} \\ y^{+}_{n,m-2} \\ y^{-}_{n,m-2} \\ y^{+}_{n,m} \\ y^{-}_{n,m} \\ y^{+}_{n,m+2} \\ y^{-}_{n,m+2} \\ y^{+}_{n,m+4} \\ y^{-}_{n,m+4} \\ \quad\vdots \end{array} \!\right]}_{\underline{x}_W(n)} \protect$](img4712.png) |
(E.32) |
and displacement output matrix
 :
:
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![\begin{displaymath}
\underbrace{\left[\!
\begin{array}{c}
\vdots \\
y_{n,m-2} \\
y_{n,m} \\
y_{n,m+2} \\
y_{n,m+4}\\
\vdots
\end{array}\!\right]}_{\underline{y}(n)}
=
\underbrace{\left[\!
\begin{array}{cccccccccc}
& \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \\
\cdots & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots\\
\cdots & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & \cdots\\
\cdots & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & \cdots\\
\cdots & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & \cdots\\
& \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots &
\end{array}\!\right]}_{\mathbf{C}_W}
\underbrace{\left[\!
\begin{array}{l}
\quad\vdots \\
y^{+}_{n,m-2} \\
y^{-}_{n,m-2} \\
y^{+}_{n,m} \\
y^{-}_{n,m} \\
y^{+}_{n,m+2} \\
y^{-}_{n,m+2} \\
y^{+}_{n,m+4} \\
y^{-}_{n,m+4} \\
\quad\vdots
\end{array}\!\right]}_{\underline{x}_W(n)}
\end{displaymath}](img4714.png)