Computational Methods

Since finding the intersection of $G(x)$ and $p_{\Delta}^{+}-x$ requires an expensive iterative algorithm with variable convergence times, it is not well suited for real-time operation. In this section, fast algorithms based on precomputed nonlinearities are described.

Let $h$ denote half-pressure $p/2$ , i.e., $h_m\isdeftext p_m/2$ and $h_{\Delta}^{+}\isdeftext p_{\Delta}^{+}/2$ . Then (9.43) becomes

$$p_b^{-}= h_m- \rho(p_{\Delta})\cdot h_{\Delta}^{+}$$ (10.45)

Subtracting this equation from $p_b^{+}$ gives

$$p_b^{+}+ \rho h_{\Delta}^{+}- h_m = p_b^{+}- p_b^{-}= p_{\Delta}- p_{\Delta}^{+}$$

$$\,\,\Rightarrow\,\, \rho h_{\Delta}^{+} = \underbrace{h_m- p_b^{+}}_{h_{\Delta}^{+}} + p_{\Delta}- 2h_{\Delta}^{+}= p_{\Delta}-h_{\Delta}^{+}$$

$$\,\,\Rightarrow\,\, \rho = \frac{p_{\Delta}}{h_{\Delta}^{+}}-1$$ (10.46)

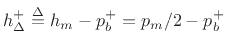The last expression above can be used to precompute $\rho$ as a function of $h_{\Delta}^{+}\isdef h_m- p_b^{+}= p_m/2 -p_b^{+}$ . Denoting this newly defined function as

$$\hat\rho (h_{\Delta}^{+}) = \rho(p_{\Delta}(h_{\Delta}^{+}))$$ (10.47)

(9.45) becomes

$$p_b^{-}= h_m- \hat\rho (h_{\Delta}^{+})\cdot h_{\Delta}^{+}$$ (10.48)

This is the form chosen for implementation in Fig. 9.39 [435]. The control variable is mouth half-pressure $h_m$ , and $h_{\Delta}^{+}=h_m-p_b^{+}$ is computed from the incoming bore pressure using only a single subtraction. The table is indexed by $h_{\Delta}^{+}$ , and the result of the lookup is then multiplied by $h_{\Delta}^{+}$ . Finally, the result of the multiplication is subtracted from $h_m$ . The cost of the reed simulation is only two subtractions, one multiplication, and one table lookup per sample.

Because the table contains a coefficient rather than a signal value, it can be more heavily quantized both in address space and word length than a direct lookup of a signal value such as $p_{\Delta}(p_{\Delta}^{+})$ or the like. A direct signal lookup, though requiring much higher resolution, would eliminate the multiplication associated with the scattering coefficient. For example, if $p_b^{+}$ and $p_b^{-}$ are 16-bit signal samples, the table would contain on the order of 64K 16-bit $p_{\Delta}^\ast$ samples. Clearly, some compression of this table would be desirable. Since $p_{\Delta}^\ast (p_{\Delta}^{+}/2)$ is smoothly varying, significant compression is in fact possible. However, because the table is directly in the signal path, comparatively little compression can be done while maintaining full audio quality (such as 16-bit accuracy).

Figure 9.42: Simple, qualitatively chosen reed table for the digital waveguide clarinet.

In the field of computer music, it is customary to use simple piecewise linear functions for functions other than signals at the audio sampling rate, e.g., for amplitude envelopes, FM-index functions, and so on [385,383]. Along these lines, good initial results were obtained [435] using the simplified qualitatively chosen reed table

$$\hat\rho (h_{\Delta}^{+}) = \left\{ \begin{array}{ll} 1-m(h_{\Delta}^c-h_{\Delta}^{+}), & -1\leq h_{\Delta}^{+}<h_{\Delta}^c\\ 1, & h_{\Delta}^c\leq h_{\Delta}^{+}\leq 1 \\ \end{array} \right.$$ (10.49)

depicted in Fig. 9.42 for $m=1/(h_{\Delta}^c+1)$ . The corner point $h_{\Delta}^c$ is the smallest pressure difference giving reed closure.^10.19 Embouchure and reed stiffness correspond to the choice of offset $h_{\Delta}^c$ and slope $m$ . Brighter tones are obtained by increasing the curvature of the function as the reed begins to open; for example, one can use $\hat\rho ^k(h_{\Delta}^{+})$ for increasing $k\geq1$ .

Another variation is to replace the table-lookup contents by a piecewise polynomial approximation. While less general, good results have been obtained in practice [89,91,92]. For example, one of the SynthBuilder [356] clarinet patches employs this technique using a cubic polynomial.

An intermediate approach between table lookups and polynomial approximations is to use interpolated table lookups. Typically, linear interpolation is used, but higher order polynomial interpolation can also be considered (see Chapter 4).