Symmetry

In the previous section, we found $\hbox{\sc Flip}(X) = \overline{X}$ when $x$ is real. This fact is of high practical importance. It says that the spectrum of every real signal is Hermitian. Due to this symmetry, we may discard all negative-frequency spectral samples of a real signal and regenerate them later if needed from the positive-frequency samples. Also, spectral plots of real signals are normally displayed only for positive frequencies; e.g., spectra of sampled signals are normally plotted over the range 0 Hz to $f_s/2$ Hz. On the other hand, the spectrum of a complex signal must be shown, in general, from $-f_s/2$ to $f_s/2$ (or from 0 to $f_s$ ), since the positive and negative frequency components of a complex signal are independent.

Recall from §7.3 that a signal $x(n)$ is said to be even if $x(-n)=x(n)$ , and odd if $x(-n)=-x(n)$ . Below are are Fourier theorems pertaining to even and odd signals and/or spectra.

Theorem: If $x\in\mathbb{R}^N$ , then re$\left\{X\right\}$ is even and im$\left\{X\right\}$ is odd.

Proof: This follows immediately from the conjugate symmetry of $X$ for real signals $x$ .

Theorem: If $x\in\mathbb{R}^N$ , $\left\vert X\right\vert$ is even and $\angle{X}$ is odd.

Proof: This follows immediately from the conjugate symmetry of $X$ expressed in polar form $X(k)= \left\vert X(k)\right\vert e^{j\angle{X(k)}}$ .

The conjugate symmetry of spectra of real signals is perhaps the most important symmetry theorem. However, there are a couple more we can readily show:

Theorem: An even signal has an even transform:

$$\zbox {x\;\mbox{even} \;\longleftrightarrow\;X\;\mbox{even}}$$

Proof: Express $x$ in terms of its real and imaginary parts by $x\isdeftext x_r + j x_i$ . Note that for a complex signal $x$ to be even, both its real and imaginary parts must be even. Then

$$X(k) \isdef \sum_{n=0}^{N-1}x(n) e^{-j\omega_k n}$$

$$= \sum_{n=0}^{N-1}[x_r(n)+jx_i(n)] \cos(\omega_k n) - j [x_r(n)+jx_i(n)] \sin(\omega_k n)$$

$$= \sum_{n=0}^{N-1}[x_r(n)\cos(\omega_k n) + x_i(n)\sin(\omega_k n)]$$

$$\;\,\mathop{+} j [x_i(n)\cos(\omega_k n) - x_r(n)\sin(\omega_k n)]. \protect$$ (7.5)

Let even$_n$ denote a function that is even in $n$ , such as $f(n)=n^2$ , and let odd$_n$ denote a function that is odd in $n$ , such as $f(n)=n^3$ , Similarly, let even$_{nk}$ denote a function of $n$ and $k$ that is even in both $n$ and $k$ , such as $f(n,k)=n^2k^2$ , and odd$_{nk}$ mean odd in both $n$ and $k$ . Then appropriately labeling each term in the last formula above gives

$$\begin{eqnarray*} X(k)&=&\sum_{n=0}^{N-1}\mbox{even}_n\cdot\mbox{even}_{nk} + \underbrace{\sum_{n=0}^{N-1}\mbox{even}_n\cdot\mbox{odd}_{nk}}_{\mbox{sums to 0}}\\ &+& j \cdot \sum_{n=0}^{N-1}\mbox{even}_n\cdot\mbox{even}_{nk} - j \underbrace{\sum_{n=0}^{N-1}{\mbox{even}_n\cdot\mbox{odd}_{nk}}}_{\mbox{sums to 0}} \\ &=&\sum_{n=0}^{N-1}\mbox{even}_n \cdot\mbox{even}_{nk} + j \cdot \sum_{n=0}^{N-1}\mbox{even}_n \cdot\mbox{even}_{nk}\\ [10pt] &=& \mbox{even}_k + j \cdot \mbox{even}_k = \mbox{even}_k. \end{eqnarray*}$$

Theorem: A real even signal has a real even transform:

$$\zbox {x\;\mbox{real and even} \;\longleftrightarrow\;X\;\mbox{real and even}}$$ (7.6)

Proof: This follows immediately from setting $x_i(n)=0$ in the preceding proof. From Eq.(7.5), we are left with

$$X(k) = \sum_{n=0}^{N-1}x_r(n)\cos(\omega_k n).$$

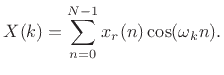
Thus, the DFT of a real and even function reduces to a type of cosine transform,^7.13

Instead of adapting the previous proof, we can show it directly:

$$\begin{eqnarray*} X(k) &\isdef & \sum_{n=0}^{N-1}x(n) e^{-j\omega_k n} = \sum_{n=0}^{N-1}x(n) \cos(\omega_k n) + j \sum_{n=0}^{N-1}x(n) \sin(\omega_k n) \\ &=& \sum_{n=0}^{N-1}x(n) \cos(\omega_k n) \quad\qquad \mbox{$\left(\sum_n\mbox{even}_n\cdot\mbox{odd}_n = \sum \mbox{odd}_n=0\right)$} \\ &=& \sum_{n=0}^{N-1}\mbox{even}_n\cdot\mbox{even}_{nk} = \sum_{n=0}^{N-1}\mbox{even}_{nk} = \mbox{even}_k \end{eqnarray*}$$

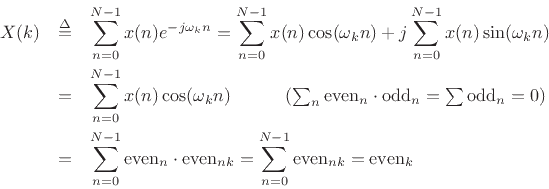
Definition: A signal with a real spectrum (such as any real, even signal) is often called a zero phase signal. However, note that when the spectrum goes negative (which it can), the phase is really $\pm\pi$ , not 0 . When a real spectrum is positive at dc (i.e., $X(0)>0$ ), it is then truly zero-phase over at least some band containing dc (up to the first zero-crossing in frequency). When the phase switches between 0 and $\pi$ at the zero-crossings of the (real) spectrum, the spectrum oscillates between being zero phase and ``constant phase''. We can say that all real spectra are piecewise constant-phase spectra, where the two constant values are 0 and $\pi$ (or $-\pi$ , which is the same phase as $+\pi$ ). In practice, such zero-crossings typically occur at low magnitude, such as in the ``side-lobes'' of the DTFT of a ``zero-centered symmetric window'' used for spectrum analysis (see Chapter 8 and Book IV [73]).