Conjugation and Reversal

Theorem: For any $x\in\mathbb{C}^N$ ,

$$\zbox {\overline{x} \;\longleftrightarrow\;\hbox{\sc Flip}(\overline{X}).}$$

Proof:

$$\begin{eqnarray*} \hbox{\sc DFT}_k(\overline{x}) &\isdef & \sum_{n=0}^{N-1}\overline{x(n)} e^{-j 2\pi nk/N} = \sum_{n=0}^{N-1}\overline{x(n) e^{j 2\pi nk/N}} \\ [5pt] &=& \overline{\sum_{n=0}^{N-1}x(n) e^{-j 2\pi n(-k)/N}} \isdef \hbox{\sc Flip}_k(\overline{X}) \end{eqnarray*}$$

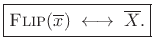
Theorem: For any $x\in\mathbb{C}^N$ ,

$$\zbox {\hbox{\sc Flip}(\overline{x}) \;\longleftrightarrow\;\overline{X}.}$$

Proof: Making the change of summation variable $m\isdeftext N-n$ , we get

$$\begin{eqnarray*} \hbox{\sc DFT}_k(\hbox{\sc Flip}(\overline{x})) &\isdef & \sum_{n=0}^{N-1}\overline{x(N-n)} e^{-j 2\pi nk/N} = \sum_{m=N}^{1} \overline{x(m)} e^{-j 2\pi (N-m)k/N} \\ &=& \sum_{m=0}^{N-1}\overline{x(m)} e^{j 2\pi m k / N} = \overline{\sum_{m=0}^{N-1}x(m) e^{-j 2\pi m k/N}} \isdef \overline{X(k)}. \end{eqnarray*}$$

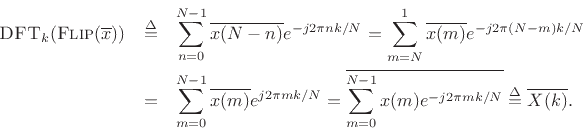
Theorem: For any $x\in\mathbb{C}^N$ ,

$$\zbox {\hbox{\sc Flip}(x) \;\longleftrightarrow\;\hbox{\sc Flip}(X).}$$

Proof:

$$\begin{eqnarray*} \hbox{\sc DFT}_k[\hbox{\sc Flip}(x)] &\isdef & \sum_{n=0}^{N-1}x(N-n) e^{-j 2\pi nk/N} = \sum_{m=0}^{N-1}x(m) e^{-j 2\pi (N-m)k/N} \\ &=& \sum_{m=0}^{N-1}x(m) e^{j 2\pi mk/N} \isdef X(-k) \isdef \hbox{\sc Flip}_k(X) \end{eqnarray*}$$

Corollary: For any $x\in\mathbb{R}^N$ ,

$$\zbox {\hbox{\sc Flip}(x) \;\longleftrightarrow\;\overline{X}}$$   $$\mbox{($x$\ real).}$$

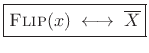
Proof: Picking up the previous proof at the third formula, remembering that $x$ is real,

$$\sum_{m=0}^{N-1}x(m) e^{j 2\pi mk/N} = \overline{\sum_{m=0}^{N-1}\overline{x(m)} e^{-j 2\pi mk/N}} = \overline{\sum_{m=0}^{N-1}x(m) e^{-j 2\pi mk/N}} \isdef \overline{X(k)}$$

when $x(m)$ is real.

Thus, conjugation in the frequency domain corresponds to reversal in the time domain. Another way to say it is that negating spectral phase flips the signal around backwards in time.

Corollary: For any $x\in\mathbb{R}^N$ ,

$$\zbox {\hbox{\sc Flip}(X) = \overline{X}}$$   $$\mbox{($x$\ real).}$$

Proof: This follows from the previous two cases.

Definition: The property $X(-k)=\overline{X(k)}$ is called Hermitian symmetry or ``conjugate symmetry.'' If $X(-k)=-\overline{X(k)}$ , it may be called skew-Hermitian.

Another way to state the preceding corollary is

$$\zbox {x\in\mathbb{R}^N\;\longleftrightarrow\;X\;\mbox{is Hermitian}.}$$