Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Linearity
Theorem: For any
 and
and
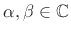 , the DFT satisfies
, the DFT satisfies
where
 and
and
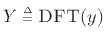 , as always in this book.
Thus, the DFT is a linear operator.
, as always in this book.
Thus, the DFT is a linear operator.
Proof:
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() and
and
![]() , the DFT satisfies
, the DFT satisfies
![\begin{eqnarray*}
\hbox{\sc DFT}_k(\alpha x + \beta y) &\isdef & \sum_{n=0}^{N-1}[\alpha x(n) + \beta y(n)]e^{-j 2\pi nk/N}\\
&=& \sum_{n=0}^{N-1}\alpha x(n)e^{-j 2\pi nk/N} + \sum_{n=0}^{N-1}\beta y(n) e^{-j 2\pi nk/N} \\
&=& \alpha \sum_{n=0}^{N-1}x(n)e^{-j 2\pi nk/N} + \beta \sum_{n=0}^{N-1}y(n) e^{-j 2\pi nk/N} \\
&\isdef & \alpha X + \beta Y
\end{eqnarray*}](img1310.png)