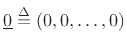 to the point
to the point
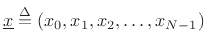 .
.
For the DFT, all signals and spectra are length ![]() . A length
. A length ![]() sequence
sequence
![]() can be denoted by
can be denoted by ![]() ,
,
![]() , where
, where ![]() may be
real (
may be
real (
![]() ) or complex (
) or complex (
![]() ). We now wish to regard
). We now wish to regard ![]() as a
vector5.1
as a
vector5.1
![]() in an
in an ![]() dimensional vector space. That is,
each sample
dimensional vector space. That is,
each sample ![]() is regarded as a coordinate in that space.
A vector
is regarded as a coordinate in that space.
A vector
![]() is mathematically a single point in
is mathematically a single point in
![]() -space represented by a list of coordinates
-space represented by a list of coordinates
![]() called an
called an ![]() -tuple. (The
notation
-tuple. (The
notation ![]() means the same thing as
means the same thing as ![]() .) It can be interpreted
geometrically as an arrow in
.) It can be interpreted
geometrically as an arrow in ![]() -space from the origin
-space from the origin
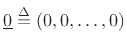 to the point
to the point
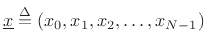 .
.
We define the following as equivalent:
![$\displaystyle x \isdef \underline{x}\isdef x(\cdot)
\isdef (x_0,x_1,\ldots,x_{N-1})
\isdef [x_0,x_1,\ldots,x_{N-1}]
\isdef [x_0\; x_1\; \cdots\; x_{N-1}]
$](img677.png)
where
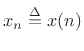 is the
is the The reader comfortable with vectors, vector addition, and vector subtraction may skip to §5.6.