Vector Addition

Given two vectors in $\mathbb{R}^N$ , say

$$\begin{eqnarray*} \underline{x}&\isdef & (x_0,x_1,\ldots,x_{N-1})\\ \underline{y}&\isdef & (y_0,y_1,\ldots,y_{N-1}), \end{eqnarray*}$$

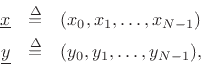
the vector sum is defined by elementwise addition. If we denote the sum by 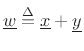$\underline{w}\isdef \underline{x}+\underline{y}$ , then we have $\underline{w}_n = x_n+y_n$ for $n=0,1,2,\ldots,N-1$ . We could also write $\underline{w}(n) = x(n)+y(n)$ for $n=0,1,2,\ldots,N-1$ if preferred.

The vector diagram for the sum of two vectors can be found using the parallelogram rule, as shown in Fig.5.2 for $N=2$ , $\underline{x}=(2,3)$ , and $\underline{y}=(4,1)$ .

Figure 5.2: Geometric interpretation of a length 2 vector sum.

Also shown are the lighter construction lines which complete the parallelogram started by $\underline{x}$ and $\underline{y}$ , indicating where the endpoint of the sum $\underline{x}+\underline{y}$ lies. Since it is a parallelogram, the two construction lines are congruent to the vectors $\underline{x}$ and $\underline{y}$ . As a result, the vector sum is often expressed as a triangle by translating the origin of one member of the sum to the tip of the other, as shown in Fig.5.3.

Figure 5.3: Vector sum, translating one vector to the tip of the other.

In the figure, $\underline{x}$ was translated to the tip of $\underline{y}$ . This depicts $y+x$ , since ``$x$ picks up where $y$ leaves off.'' It is equally valid to translate $\underline{y}$ to the tip of $\underline{x}$ , because vector addition is commutative, i.e., $\underline{x}+\underline{y}$ = $\underline{y}+\underline{x}$ .