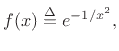
Consider the inverted Gaussian pulse,E.1
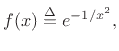
i.e.,
As mentioned in §E.2, a measure of ``flatness'' is the number
of leading zero terms in a function's Taylor expansion (not counting
the first (constant) term). Thus, by this measure, the bell curve is
``infinitely flat'' at infinity, or, equivalently, ![]() is
infinitely flat at
is
infinitely flat at ![]() .
.
Another property of
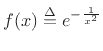 is that it has an
infinite number of ``zeros'' at
is that it has an
infinite number of ``zeros'' at ![]() . The fact that a function
. The fact that a function
![]() has an infinite number of zeros at
has an infinite number of zeros at ![]() can be verified by
showing
can be verified by
showing
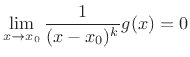
for all
for any integer
The reciprocal of a function containing an infinite-order zero at
![]() has what is called an essential singularity at
has what is called an essential singularity at ![]() [16, p. 157], also called a
non-removable
singularity. Thus,
[16, p. 157], also called a
non-removable
singularity. Thus,
![]() has an essential
singularity at
has an essential
singularity at ![]() , and
, and ![]() has one at
has one at ![]() .
.
An amazing result from the theory of complex variables
[16, p. 270]
is that near an essential singular point
![]() (i.e.,
(i.e., ![]() may be
a complex number), the inequality
may be
a complex number), the inequality
is satisfied at some point
In summary, a Taylor series expansion about the point ![]() will
always yield a constant approximation when the function being
approximated is infinitely flat at
will
always yield a constant approximation when the function being
approximated is infinitely flat at ![]() . For this reason, polynomial
approximations are often applied over a restricted range of
. For this reason, polynomial
approximations are often applied over a restricted range of ![]() , with
constraints added to provide transitions from one interval to the
next. This leads to the general subject of splines
[84]. In particular, cubic spline approximations
are composed of successive segments which are each third-order polynomials. In each segment,
four degrees of freedom are available (the four polynomial
coefficients). Two of these are usually devoted to matching the
amplitude and slope of the polynomial to one side, while the other two
are used to maximize some measure of fit across the segment. The
points at which adjacent polynomial segments connect are called
``knots'', and finding optimal knot locations is usually a relatively
expensive, iterative computation.
, with
constraints added to provide transitions from one interval to the
next. This leads to the general subject of splines
[84]. In particular, cubic spline approximations
are composed of successive segments which are each third-order polynomials. In each segment,
four degrees of freedom are available (the four polynomial
coefficients). Two of these are usually devoted to matching the
amplitude and slope of the polynomial to one side, while the other two
are used to maximize some measure of fit across the segment. The
points at which adjacent polynomial segments connect are called
``knots'', and finding optimal knot locations is usually a relatively
expensive, iterative computation.