Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
The dual of the zero-padding theorem states formally that
zero padding in the frequency domain corresponds to periodic
interpolation in the time domain:
Definition: For all
 and any integer
and any integer 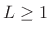 ,
,
 |
(7.7) |
where zero padding is defined in §7.2.7 and illustrated in
Figure 7.7. In other words, zero-padding a DFT by the factor  in
the frequency domain
(by inserting
in
the frequency domain
(by inserting 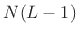 zeros at bin number
zeros at bin number 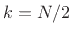 corresponding to
the folding frequency7.22)
gives rise to ``periodic interpolation'' by the factor
corresponding to
the folding frequency7.22)
gives rise to ``periodic interpolation'' by the factor  in the time
domain. It is straightforward to show that the interpolation kernel
used in periodic interpolation is an aliased sinc function,
that is, a sinc function
in the time
domain. It is straightforward to show that the interpolation kernel
used in periodic interpolation is an aliased sinc function,
that is, a sinc function
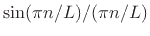 that has been
time-aliased on a block of length
that has been
time-aliased on a block of length 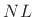 . Such an aliased sinc function
is of course periodic with period
. Such an aliased sinc function
is of course periodic with period 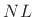 samples. See Appendix D
for a discussion of ideal bandlimited interpolation, in which
the interpolating sinc function is not aliased.
samples. See Appendix D
for a discussion of ideal bandlimited interpolation, in which
the interpolating sinc function is not aliased.
Periodic interpolation is ideal for signals that are periodic
in 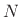 samples, where
samples, where 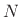 is the DFT length. For non-periodic
signals, which is almost always the case in practice, bandlimited
interpolation should be used instead (Appendix D).
is the DFT length. For non-periodic
signals, which is almost always the case in practice, bandlimited
interpolation should be used instead (Appendix D).
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() and any integer
and any integer ![]() ,
,
![]() samples, where
samples, where ![]() is the DFT length. For non-periodic
signals, which is almost always the case in practice, bandlimited
interpolation should be used instead (Appendix D).
is the DFT length. For non-periodic
signals, which is almost always the case in practice, bandlimited
interpolation should be used instead (Appendix D).