Our first example is an FFT of the simple sinusoid
where we choose
% Example 1: FFT of a DFT-sinusoid
% Parameters:
N = 64; % Must be a power of two
T = 1; % Set sampling rate to 1
A = 1; % Sinusoidal amplitude
phi = 0; % Sinusoidal phase
f = 0.25; % Frequency (cycles/sample)
n = [0:N-1]; % Discrete time axis
x = A*cos(2*pi*n*f*T+phi); % Sampled sinusoid
X = fft(x); % Spectrum
% Plot time data:
figure(1);
subplot(3,1,1);
plot(n,x,'*k');
ni = [0:.1:N-1]; % Interpolated time axis
hold on;
plot(ni,A*cos(2*pi*ni*f*T+phi),'-k'); grid off;
title('Sinusoid at 1/4 the Sampling Rate');
xlabel('Time (samples)');
ylabel('Amplitude');
text(-8,1,'a)');
hold off;
% Plot spectral magnitude:
magX = abs(X);
fn = [0:1/N:1-1/N]; % Normalized frequency axis
subplot(3,1,2);
stem(fn,magX,'ok'); grid on;
xlabel('Normalized Frequency (cycles per sample))');
ylabel('Magnitude (Linear)');
text(-.11,40,'b)');
% Same thing on a dB scale:
spec = 20*log10(magX); % Spectral magnitude in dB
subplot(3,1,3);
plot(fn,spec,'--ok'); grid on;
axis([0 1 -350 50]);
xlabel('Normalized Frequency (cycles per sample))');
ylabel('Magnitude (dB)');
text(-.11,50,'c)');
cmd = ['print -deps ', '../eps/example1.eps'];
disp(cmd); eval(cmd);
![\includegraphics[width=\twidth]{eps/example1}](img1485.png) |
The results are shown in Fig.8.1. The time-domain signal is
shown in the upper plot (Fig.8.1a), both in pseudo-continuous
and sampled form. In the middle plot (Fig.8.1b), we see two
peaks in the magnitude spectrum, each at magnitude ![]() on a linear
scale, located at normalized frequencies
on a linear
scale, located at normalized frequencies ![]() and
and
![]() . A spectral peak amplitude of
. A spectral peak amplitude of
![]() is what we
expect, since
is what we
expect, since
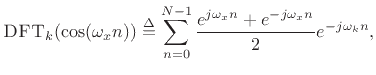
and when
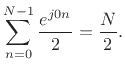
For
The spectrum should be exactly zero at the other bin numbers. How
accurately this happens can be seen by looking on a dB scale, as shown in
Fig.8.1c. We see that the spectral magnitude in the other bins is
on the order of ![]() dB lower, which is close enough to zero for audio
work
dB lower, which is close enough to zero for audio
work
![]() .
.