
A function related to cross-correlation is the coherence function, defined in terms of power spectral densities and the cross-spectral density by

In practice, these quantities can be estimated by time-averaging
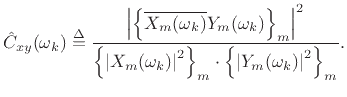
Note that the averaging in the numerator occurs before the absolute value is taken.
The coherence
![]() is a real function between zero and one
which gives a measure of correlation between
is a real function between zero and one
which gives a measure of correlation between ![]() and
and ![]() at
each frequency
at
each frequency ![]() . For example, imagine that
. For example, imagine that ![]() is produced
from
is produced
from ![]() via an LTI filtering operation:
via an LTI filtering operation:
Then the magnitude-normalized cross-spectrum in each frame is
![\begin{eqnarray*}
{\hat A}_{x_m y_m}(\omega_k) &\isdef &
\frac{\overline{X_m(\omega_k)}Y_m(\omega_k)}{\left\vert X_m(\omega_k)\right\vert\cdot\left\vert Y_m(\omega_k)\right\vert}
= \frac{\overline{X_m(\omega_k)}H(\omega_k)X_m(\omega_k)}{\left\vert X_m(\omega_k)\right\vert\cdot\left\vert H(\omega_k)X_m(\omega_k)\right\vert}\\ [5pt]
&=& \frac{\left\vert X_m(\omega_k)\right\vert^2 H(\omega_k)}{\left\vert X_m(\omega_k)\right\vert^2\left\vert H(\omega_k)\right\vert}
= \frac{H(\omega_k)}{\left\vert H(\omega_k)\right\vert}
\end{eqnarray*}](img1604.png)
so that the coherence function becomes
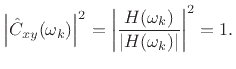
On the other hand, when
A common use for the coherence function is in the validation of
input/output data collected in an acoustics experiment for purposes of
system identification. For example, ![]() might be a known
signal which is input to an unknown system, such as a reverberant
room, say, and
might be a known
signal which is input to an unknown system, such as a reverberant
room, say, and ![]() is the recorded response of the room. Ideally,
the coherence should be
is the recorded response of the room. Ideally,
the coherence should be ![]() at all frequencies. However, if the
microphone is situated at a null in the room response for some
frequency, it may record mostly noise at that frequency. This is
indicated in the measured coherence by a significant dip below 1. An
example is shown in Book III [72] for the case of a measured
guitar-bridge admittance.
A more elementary example is given in the next section.
at all frequencies. However, if the
microphone is situated at a null in the room response for some
frequency, it may record mostly noise at that frequency. This is
indicated in the measured coherence by a significant dip below 1. An
example is shown in Book III [72] for the case of a measured
guitar-bridge admittance.
A more elementary example is given in the next section.