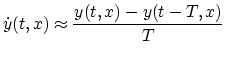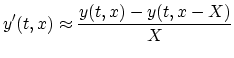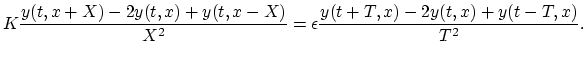Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
The classical physical model for transverse vibrations in an ideal
string, as illustrated in Fig. 3, is the following
wave equation
[110,111,118,180]:5
where
(Note that ``
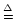 '' means ``is defined as''.)
Applying the
finite difference approximation (FDA) means to replace each
partial derivative by a finite difference [169], e.g.,
and
where
'' means ``is defined as''.)
Applying the
finite difference approximation (FDA) means to replace each
partial derivative by a finite difference [169], e.g.,
and
where 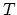 and
and 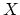 are the time and position sampling intervals to
be used, respectively. Note that the finite-difference approximations
become exact, in the limit, as
are the time and position sampling intervals to
be used, respectively. Note that the finite-difference approximations
become exact, in the limit, as 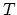 and
and 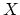 approach zero. In
practice, more accurate simulation is obtained with increasing
sampling rates. Applying a FDA to the ideal string wave equation above
yields
Normalizing
approach zero. In
practice, more accurate simulation is obtained with increasing
sampling rates. Applying a FDA to the ideal string wave equation above
yields
Normalizing 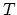 ,
, 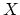 , and
, and
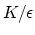 to 1 leads to the simplified recursion
Thus, for each time step
to 1 leads to the simplified recursion
Thus, for each time step 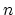 , the string position samples can be
updated using all samples along the string from the previous two time
steps. The FDA method for numerical string simulation was used by
Pierre Ruiz in his early work on vibrating-string simulation
[74,131], and it is still in use today
[31,32,49].
, the string position samples can be
updated using all samples along the string from the previous two time
steps. The FDA method for numerical string simulation was used by
Pierre Ruiz in his early work on vibrating-string simulation
[74,131], and it is still in use today
[31,32,49].
Perhaps surprisingly, it can be shown that the above recursion is
exact at the sample points, despite the apparent crudeness
of the finite difference approximation at low sampling rates, provided
the string initial conditions and excitations are bandlimited
to less than half the sampling rate. An easy proof is based on
showing its equivalence to the digital waveguide model for the
ideal string [159, pp. 430-431].
Subsections
Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download jnmr.pdf
![\includegraphics[width=5in]{eps/Fphysicalstring.eps}](img4.png)