Every causal stable filter ![]() with no zeros on the unit
circle can be factored into a minimum-phase filter in cascade with a
causal stable allpass filter:
with no zeros on the unit
circle can be factored into a minimum-phase filter in cascade with a
causal stable allpass filter:
where
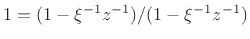
and
This result is easy to show by induction. Consider a single
maximum-phase zero ![]() of
of ![]() . Then
. Then
![]() , and
, and ![]() can be written with the maximum-phase zero factored out as
can be written with the maximum-phase zero factored out as
Now multiply by
We have thus factored
In summary, we may factor maximum-phase zeros out of the transfer function and replace them with their minimum-phase counterparts without altering the amplitude response. This modification is equivalent to placing a stable allpass filter in series with the original filter, where the allpass filter cancels the maximum-phase zero and introduces the minimum-phase zero.
A procedure for computing the minimum phase for a given spectral magnitude is discussed in §11.7 below. More theory pertaining to minimum phase sequences may be found in [60].