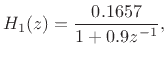
Figure 3.13 shows the impulse response of the real one-pole section
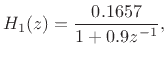
and Fig.3.14 shows its frequency response, computed using the matlab utility myfreqz listed in Fig.7.1. (Both Matlab and Octave have compatible utilities freqz, which serve the same purpose.) Note that the sampling rate is set to 1, and the frequency axis goes from 0 Hz all the way to the sampling rate, which is appropriate for complex filters (as we will soon see). Since real filters have Hermitian frequency responses (i.e., an even amplitude response and odd phase response), they may be plotted from 0 Hz to half the sampling rate without loss of information.
Figure 3.15 shows the impulse response of the complex one-pole section
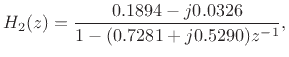
and Fig.3.16 shows the corresponding frequency response.
![\includegraphics[width=\twidth]{eps/arcir2}](img363.png) |
The complex-conjugate section,

is of course quite similar, and is shown in Figures 3.17 and 3.18.
![\includegraphics[width=\twidth]{eps/arcir3}](img366.png) |
Figure 3.19 shows the impulse response of the complex one-pole section
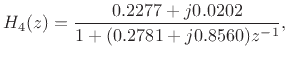
and Fig.3.20 shows its frequency response. Its complex-conjugate counterpart is not shown since it is analogous to
![\includegraphics[width=\twidth]{eps/arcir4}](img370.png) |