In practice, we usually work with a sampled frequency axis. That
is, instead of evaluating the transfer function
![]() at
at
![]() to obtain the frequency response
to obtain the frequency response
![]() , where
, where ![]() is continuous radian frequency, we compute instead
is continuous radian frequency, we compute instead
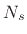
where
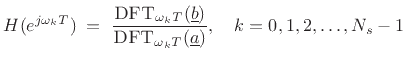
The uniformly sampled DTFT has its own name: the discrete Fourier transform (DFT) [84]. Thus, we can write
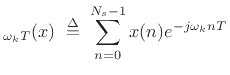
where
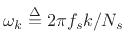
and
 , where
, where
To avoid undersampling
![]() , we must have
, we must have ![]() , and to
avoid undersampling
, and to
avoid undersampling
![]() , we must have
, we must have ![]() . In general,
. In general,
![]() will be undersampled (when
will be undersampled (when ![]() ), because it is the
quotient of
), because it is the
quotient of
![]() over
over
![]() . This means, for example, that
computing the impulse response
. This means, for example, that
computing the impulse response ![]() from the sampled frequency
response
from the sampled frequency
response
![]() will be time aliased in general. I.e.,
will be time aliased in general. I.e.,

will be time-aliased in the IIR case. In other words, an infinitely long impulse response cannot be Fourier transformed using a finite-length DFT, and this corresponds to not being able to sample the frequency response of an IIR filter without some loss of information. In practice, we simply choose
As is well known, when the DFT length ![]() is a power of 2, e.g.,
is a power of 2, e.g.,
![]() , the DFT can be computed extremely efficiently using
the Fast Fourier Transform (FFT). Figure 7.1 gives an
example matlab script for computing the frequency response of an IIR
digital filter using two FFTs. The matlab function freqz
also uses this method when possible (e.g., when
, the DFT can be computed extremely efficiently using
the Fast Fourier Transform (FFT). Figure 7.1 gives an
example matlab script for computing the frequency response of an IIR
digital filter using two FFTs. The matlab function freqz
also uses this method when possible (e.g., when ![]() is a power of 2).
is a power of 2).
function [H,w] = myfreqz(B,A,N,whole,fs) %MYFREQZ Frequency response of IIR filter B(z)/A(z). % N = number of uniform frequency-samples desired % H = returned frequency-response samples (length N) % w = frequency axis for H (length N) in radians/sec % Compatible with simple usages of FREQZ in Matlab. % FREQZ(B,A,N,whole) uses N points around the whole % unit circle, where 'whole' is any nonzero value. % If whole=0, points go from theta=0 to pi*(N-1)/N. % FREQZ(B,A,N,whole,fs) sets the assumed sampling % rate to fs Hz instead of the default value of 1. % If there are no output arguments, the amplitude and % phase responses are displayed. Poles cannot be % on the unit circle. A = A(:).'; na = length(A); % normalize to row vectors B = B(:).'; nb = length(B); if nargin < 3, N = 1024; end if nargin < 4, if isreal(b) & isreal(a), whole=0; else whole=1; end; end if nargin < 5, fs = 1; end Nf = 2*N; if whole, Nf = N; end w = (2*pi*fs*(0:Nf-1)/Nf)'; H = fft([B zeros(1,Nf-nb)]) ./ fft([A zeros(1,Nf-na)]); if whole==0, w = w(1:N); H = H(1:N); end if nargout==0 % Display frequency response if fs==1, flab = 'Frequency (cyles/sample)'; else, flab = 'Frequency (Hz)'; end subplot(2,1,1); % In octave, labels go before plot: plot([0:N-1]*fs/N,20*log10(abs(H)),'-k'); grid('on'); xlabel(flab'); ylabel('Magnitude (dB)'); subplot(2,1,2); plot([0:N-1]*fs/N,angle(H),'-k'); grid('on'); xlabel(flab); ylabel('Phase'); end |