Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Figure 3.21 shows the impulse response of the real two-pole section
and Fig.3.22 shows its frequency response. The frequency axis
unnecessarily extends all the way to the sampling rate (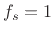 ).
).
Figure 3.22:
Frequency response of real
two-pole section 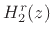 .
.
![\includegraphics[width=\twidth]{eps/arfr2}](img375.png) |
Finally, Fig.3.23 gives the impulse response of the real two-pole
section
and Fig.3.24 its frequency response.
Figure 3.23:
Impulse response of real two-pole
section 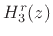 of the real partial-fraction-expansion of the example
filter.
of the real partial-fraction-expansion of the example
filter.
![\includegraphics[width=\twidth]{eps/arir3}](img377.png) |
Figure 3.24:
Frequency response of real
two-pole section 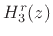 .
.
![\includegraphics[width=\twidth]{eps/arfr3}](img378.png) |
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
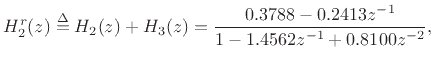
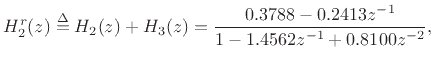
![\includegraphics[width=\twidth]{eps/arir2}](img374.png)
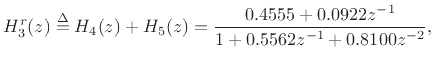
![\includegraphics[width=\twidth]{eps/arir3}](img377.png)