Another well known rule of thumb is that the ![]() of a resonator is the
number of ``periods'' under the exponential decay of its impulse
response with time-constant
of a resonator is the
number of ``periods'' under the exponential decay of its impulse
response with time-constant
![]() . More
precisely, we will show that, for
. More
precisely, we will show that, for ![]() , the impulse response
decays by the factor
, the impulse response
decays by the factor ![]() in
in ![]() cycles, which is about 96
percent decay, or -27 dB.
cycles, which is about 96
percent decay, or -27 dB.
The impulse response corresponding to Eq.(E.7) is found by
inverting the Laplace transform of the transfer function ![]() . Since it
is only second order, the solution can be found in many tables of
Laplace transforms. Alternatively, we can break it up into a sum of
first-order terms which are invertible by inspection (possibly after
rederiving the Laplace transform of an exponential decay, which is
very simple). Thus we perform the partial fraction expansion of
Eq.(E.7) to obtain
. Since it
is only second order, the solution can be found in many tables of
Laplace transforms. Alternatively, we can break it up into a sum of
first-order terms which are invertible by inspection (possibly after
rederiving the Laplace transform of an exponential decay, which is
very simple). Thus we perform the partial fraction expansion of
Eq.(E.7) to obtain
where
| (E.10) | |||
| (E.11) |
The impulse response is thus
Assuming a resonator, ![]() , we have
, we have
![]() , where
, where
![]() (using notation of the
preceding section), and the impulse response reduces to
(using notation of the
preceding section), and the impulse response reduces to
where
We have shown so far that the impulse response ![]() decays as
decays as
![]() with a sinusoidal radian frequency
with a sinusoidal radian frequency ![]() under the exponential envelope. After Q periods at frequency
under the exponential envelope. After Q periods at frequency
![]() , time has advanced to
, time has advanced to

where we have used the definition Eq.(E.8)
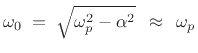 .
Thus, after
.
Thus, after
which is about 96 percent decay. The only approximation in this derivation was
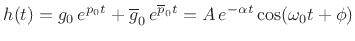
which holds whenever