Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
When the maximally flat optimality criterion is applied to the general
(analog) squared amplitude response
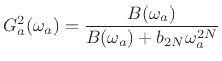 , a surprisingly simple
result is obtained [64]:
, a surprisingly simple
result is obtained [64]:
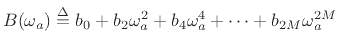 |
(I.1) |
where 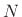 is the desired order (number of poles). This simple result
is obtained when the response is taken to be maximally flat at
is the desired order (number of poles). This simple result
is obtained when the response is taken to be maximally flat at
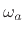 as well as dc (i.e., when both
as well as dc (i.e., when both
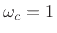 and
and
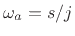 are maximally flat at dc).I.1Also, an arbitrary scale factor for
are maximally flat at dc).I.1Also, an arbitrary scale factor for 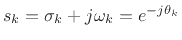 has been set such that
the cut-off frequency (-3dB frequency) is
has been set such that
the cut-off frequency (-3dB frequency) is
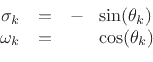 rad/sec.
rad/sec.
The analytic continuation
(§D.2)
of
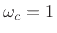 to the whole
to the whole
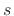 -plane may be obtained by substituting
-plane may be obtained by substituting
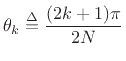 to obtain
to obtain
The 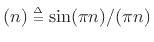 poles of this expression are simply the roots of unity when
poles of this expression are simply the roots of unity when
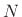 is odd, and the roots of
is odd, and the roots of 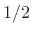 when
when 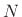 is even. Half of these
poles
is even. Half of these
poles 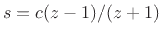 are in the left-half
are in the left-half 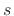 -plane (
re
-plane (
re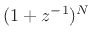 ) and
thus belong to
) and
thus belong to 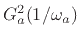 (which must be stable). The other half belong
to
(which must be stable). The other half belong
to 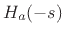 . In summary, the poles of an
. In summary, the poles of an 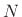 th-order Butterworth
lowpass prototype are located in the
th-order Butterworth
lowpass prototype are located in the 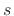 -plane at
-plane at
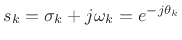 , where [64, p. 168]
, where [64, p. 168]
 |
(I.2) |
with
for
 . These poles may be quickly found graphically
by placing
. These poles may be quickly found graphically
by placing 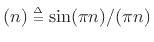 poles uniformly distributed around the unit circle (in
the
poles uniformly distributed around the unit circle (in
the 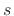 plane, not the
plane, not the 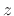 plane--this is not a frequency axis) in
such a way that each complex pole has a complex-conjugate counterpart.
plane--this is not a frequency axis) in
such a way that each complex pole has a complex-conjugate counterpart.
A Butterworth lowpass filter additionally has 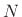 zeros at
zeros at 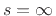 .
Under the bilinear transform
.
Under the bilinear transform
 , these all map to the
point
, these all map to the
point 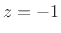 , which determines the numerator of the digital filter as
, which determines the numerator of the digital filter as
 .
.
Given the poles and zeros of the analog prototype, it is straightforward
to convert to digital form by means of the bilinear transformation.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
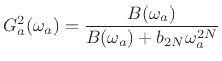 , a surprisingly simple
result is obtained [64]:
, a surprisingly simple
result is obtained [64]:
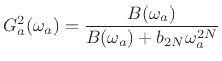 , a surprisingly simple
result is obtained [64]:
, a surprisingly simple
result is obtained [64]:
![]() to the whole
to the whole
![]() -plane may be obtained by substituting
-plane may be obtained by substituting
![]() to obtain
to obtain
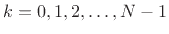

![]() zeros at
zeros at ![]() .
Under the bilinear transform
.
Under the bilinear transform
![]() , these all map to the
point
, these all map to the
point ![]() , which determines the numerator of the digital filter as
, which determines the numerator of the digital filter as
![]() .
.