Example: Second-Order Butterworth Lowpass

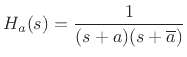
In the second-order case, we have, for the analog prototype,

$$H_a(s) = \frac{1}{(s + a)(s + \overline{a})}$$

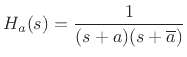
where, from Eq.(I.2), $a = e^{j\pi/4}$ , so that

$$H_a(s) = \frac{1}{(s + e^{j\pi/4})(s + e^{-j\pi/4})} = \frac{1}{s^2 + \sqrt{2}s + 1} \protect$$ (I.3)

To convert this to digital form, we apply the bilinear transform

$$s = c\frac{1-z^{-1}}{1+z^{-1}}$$

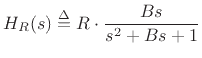
(from Eq.(I.9)), where, as discussed in §I.3, we set

$$c = \cot(\omega_cT/2) \isdef \frac{\cos(\omega_cT/2)}{\sin(\omega_cT/2)}$$

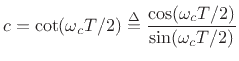
to obtain a digital cut-off frequency at $\omega_c$ radians per second. For example, choosing $\omega_c T = \pi/2$ (a cut off at one-fourth the sampling rate), we get

$$c = \frac{\cos(\pi/4)}{\sin(\pi/4)} = 1$$

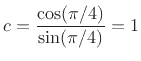
and the digital filter transfer function is

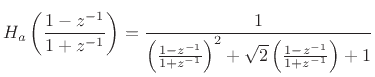$$H_d(z) = H_a\left(\frac{1-z^{-1}}{1+z^{-1}}\right) = \frac{1}{\left(\frac{1-z^{-1}}{1+z^{-1}}\right)^2 + \sqrt{2}\left(\frac{1-z^{-1}}{1+z^{-1}}\right) + 1}$$ (I.4)

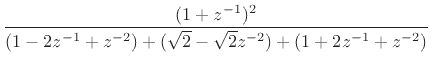$$= \frac{(1+z^{-1})^2}{(1-2z^{-1}+z^{-2}) + (\sqrt{2} - \sqrt{2}z^{-2}) + (1+2z^{-1}+z^{-2})}$$ (I.5)

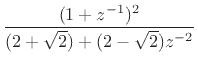$$= \frac{(1+z^{-1})^2}{(2+\sqrt{2}) + (2-\sqrt{2})z^{-2}}$$ (I.6)

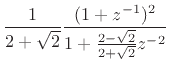$$= \frac{1}{2+\sqrt{2}}\frac{(1+z^{-1})^2}{1 + \frac{2-\sqrt{2}}{2+\sqrt{2}}z^{-2}}$$ (I.7)

Note that the numerator is $(1+z^{-1})^2$ , as predicted earlier. As a check, we can verify that the dc gain is 1:

$$H_d(1) = \frac{2^2}{2+\sqrt{2} + 2-\sqrt{2}} = 1$$

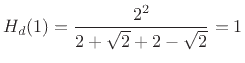
It is also immediately verified that $H_d(-1) = 0$ , i.e., that there is a (double) notch at half the sampling rate.

In the analog prototype, the cut-off frequency is $\omega_a=1$ rad/sec, where, from Eq.(I.1), the amplitude response is $G_a(j)=1/\sqrt{2}$ . Since we mapped the cut-off frequency precisely under the bilinear transform, we expect the digital filter to have precisely this gain. The digital frequency response at one-fourth the sampling rate is

$$H_d(j) = \frac{(1-j)^2}{2+\sqrt{2} - (2-\sqrt{2})} = -\frac{j}{\sqrt{2}}, \protect$$ (I.8)

and $20\log_{10}(\left\vert H_d(j)\right\vert)=-3$ dB as expected.

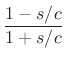Note from Eq.(I.8) that the phase at cut-off is exactly -90 degrees in the digital filter. This can be verified against the pole-zero diagram in the $z$ plane, which has two zeros at $z = -1$ , each contributing +45 degrees, and two poles at $z=\pm j\sqrt{\frac{2-\sqrt{2}}{2+\sqrt{2}}}$ , each contributing -90 degrees. Thus, the calculated phase-response at the cut-off frequency agrees with what we expect from the digital pole-zero diagram.

In the $s$ plane, it is not as easy to use the pole-zero diagram to calculate the phase at $\omega_a=1$ , but using Eq.(I.3), we quickly obtain

$$H_a(j\cdot 1) = \frac{1}{j^2 + \sqrt{2}j + 1} = -\frac{j}{\sqrt{2}},$$

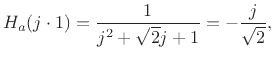
and exact agreement with $H_d(e^{j\pi/2})$ [Eq.(I.8)] is verified.

A related example appears in §9.2.4.