Zero-Phase Filters
(Even Impulse Responses)

A zero-phase filter is a special case of a linear-phase filter in which the phase slope is $\alpha=0$. The real impulse response $h(n)$ of a zero-phase filter is even.^11.1 That is, it satisfies

$$h(n) = h(-n), \quad n\in{\bf Z}$$

Note that every even signal is symmetric, but not every symmetric signal is even. To be even, it must be symmetric about time 0.

A zero-phase filter cannot be causal (except in the trivial case when the filter is a constant scale factor $h(n)=g\delta(n)$). However, in many ``off-line'' applications, such as when filtering a sound file on a computer disk, causality is not a requirement, and zero-phase filters are often preferred.

It is a well known Fourier symmetry that real, even signals have real, even Fourier transforms [84]. Therefore,

$\parbox{0.8\textwidth}{\emph{a real, even impulse response corresponds to a real, \\ even frequency response.}}$

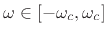
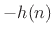
This follows immediately from writing the DTFT of $h$ in terms of a cosine and sine transform:

$$H(e^{j\omega T}) \eqsp$$   DTFT$$_{\omega T}(h) \eqsp \sum_{n=-\infty}^\infty h(n) \cos(\omega nT) - j \sum_{n=-\infty}^\infty h(n) \sin(\omega nT)$$

Since $h$ is even, cosine is even, and sine is odd; and since even times even is even, and even times odd is odd; and since the sum over an odd function is zero, we have that

$$H(e^{j\omega T}) \eqsp \sum_{n=-\infty}^\infty h(n) \cos(\omega nT)$$

for any real, even impulse-response $h$. Thus, the frequency response $H(e^{j\omega T})$ is a real, even function of $\omega$.

A real frequency response has phase zero when it is positive, and phase $\pi$ when it is negative. Therefore, we define a zero-phase filter as follows:

$\parbox{0.8\textwidth}{A filter is said to be \emph{zero phase} when... ... frequency $\omega$, and when $H(e^{j\omega T})>0$\ in the filter passband(s).}$

Recall from §7.5.2 that a passband is defined as a frequency band that is ``passed'' by the filter, i.e., the filter is not designed to minimize signal amplitude in the band. For example, in a lowpass filter with cut-off frequency $\omega_c$ rad/s, the passband is $\omega\in[-\omega_c,\omega_c]$.