
Since z transforming the convolution representation for digital filters was so fruitful, let's apply it now to the general difference equation, Eq.(5.1). To do this requires two properties of the z transform, linearity (easy to show) and the shift theorem (derived in §6.3 above). Using these two properties, we can write down the z transform of any difference equation by inspection, as we now show. In §6.8.2, we'll show how to invert by inspection as well.
Repeating the general difference equation for LTI filters, we have
(from Eq.(5.1))

Let's take the z transform of both sides, denoting the transform by
![]() . Because
. Because
![]() is a linear operator,
it may be distributed through the terms on the right-hand side as
follows:7.3
is a linear operator,
it may be distributed through the terms on the right-hand side as
follows:7.3![\begin{eqnarrayda}
{\cal Z}_z\{y(\cdot)\}
&=& {\cal Z}\{ b_0 x(n) &+& b_1 x(n - 1) + \cdots + b_M x(n - M)\\
& & &-& a_1 y(n - 1) - \cdots - a_N y(n - N)\}\\ [5pt]
&=& {\cal Z}\{ b_0 x(n)\} &+& {\cal Z}\{b_1 x(n - 1)\} + \cdots + {\cal Z}\{b_M x(n - M)\}\\
& & &-& {\cal Z}\{a_1 y(n - 1)\} - \cdots - {\cal Z}\{a_N y(n - N)\}\\ [5pt]
&=& b_0{\cal Z}\{ x(n)\} &+& b_1{\cal Z}\{x(n - 1)\} + \cdots + b_M{\cal Z}\{x(n - M)\}\\
& & &-& a_1{\cal Z}\{y(n - 1)\} - \cdots - a_N{\cal Z}\{y(n - N)\}\\ [5pt]
&=& b_0 X(z) &+& b_1 z^{-1}X(z) + \cdots + b_M z^{-M} X(z)\\
& & &-& a_1 z^{-1}Y(z) - \cdots - a_N z^{-N} Y(z),
\end{eqnarrayda}](img663.png) where we used the superposition and scaling properties of linearity
given on page
where we used the superposition and scaling properties of linearity
given on page ![]() , followed by use of the shift
theorem, in that order. The terms in
, followed by use of the shift
theorem, in that order. The terms in ![]() may be grouped together
on the left-hand side to get
may be grouped together
on the left-hand side to get
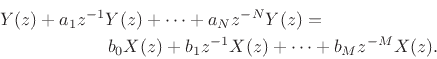
Factoring out the common terms ![]() and
and ![]() gives
gives
Defining the polynomials
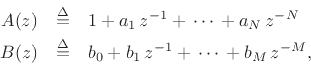
the z transform of the difference equation yields
Finally, solving for