Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Factored Form
By the fundamental theorem of algebra, every  th order polynomial
can be factored into a product of
th order polynomial
can be factored into a product of  first-order polynomials.
Therefore, Eq.(6.5) above can be written in
factored form as
first-order polynomials.
Therefore, Eq.(6.5) above can be written in
factored form as
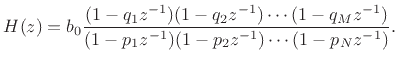 |
(7.6) |
The numerator roots
 are called the zeros
of the transfer function, and the denominator roots
are called the zeros
of the transfer function, and the denominator roots
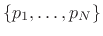 are called the poles of the filter. Poles and zeros are
discussed further in Chapter 8.
are called the poles of the filter. Poles and zeros are
discussed further in Chapter 8.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() th order polynomial
can be factored into a product of
th order polynomial
can be factored into a product of ![]() first-order polynomials.
Therefore, Eq.(6.5) above can be written in
factored form as
first-order polynomials.
Therefore, Eq.(6.5) above can be written in
factored form as