Symmetric Linear-Phase Filters

As stated at the beginning of this chapter, the impulse response of every causal, linear-phase, FIR filter is symmetric:

$$h(n) = h(N-1-n), \quad n=0,1,2,\ldots,N-1.$$

Assume that $N$ is odd. Then the filter

$$h_{\hbox{\tiny zp}}(n) = h\left(n+\frac{N-1}{2}\right), \quad n=-\frac{N-1}{2},\,\ldots\,,\frac{N-1}{2}$$

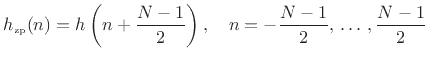
is a zero-phase filter. Thus, every odd-length linear-phase filter can be expressed as a delay of some zero-phase filter,

$$h(n) = h_{\hbox{\tiny zp}}\left(n-\frac{N-1}{2}\right), \quad n=0,1,2,\ldots, N-1.$$

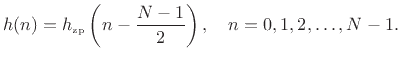
By the shift theorem for z transforms (§6.3), the transfer function of a linear-phase filter is

$$H(z) = z^{-\frac{N-1}{2}}H_{\hbox{zp}}(z)$$

and the frequency response is

$$H(e^{j\omega T}) = e^{-j\omega \frac{N-1}{2}T}H_{\hbox{zp}}(e^{j\omega T})$$

which is a linear phase term times $H_{\hbox{zp}}(e^{j\omega T})$ which is real. Since $H_{\hbox{zp}}(e^{j\omega T})$ can go negative, the phase response is

$$\Theta(\omega) = \left\{\begin{array}{ll} \displaystyle-\frac{N-... ...-1}{2}\omega T + \pi, & H_{\hbox{zp}}(e^{j\omega T})<0 \\ \end{array}\right..$$

For frequencies $\omega$ at which $H_{\hbox{zp}}(e^{j\omega T})$ is nonnegative, the phase delay and group delay of a linear-phase filter are simply half its length:

$$\begin{array}{rclrcl} P(\omega) &\isdef & -\displaystyle\fra... ...2} T, \qquad H_{\hbox{zp}}(e^{j\omega T})\geq0\\ \end{array}$$